Question

【题目】奇函数f（x）定义域是（﹣1，0）∪（0，1），f（）＝0，当x＞0时，总有（x）f′（x）ln（1﹣x2）＞2f（x）成立，则不等式f（x）＞0的解集为（　　）

A. B.

C. D.

Answer 1

【答案】B

【解析】

把已知条件（x）f′（x）ln（1﹣x2）＞2f（x）变形为f′（x）ln（1﹣x2）0，可想到构造函数g（x）＝f（x）ln（1﹣x2）并判断其单调性，结合f（）＝f（）＝0，得g（）＝g（）＝0，由单调性可得，在（﹣1，），（0，）上，g（x）＜0，而ln（1﹣x2）＜0，则f（x）＞0成立，答案可求．

∵当x＞0时，总有（x）f′（x）ln（1﹣x2）＞2f（x）成立，即f′（x）ln（1﹣x2）成立，也就是f′（x）ln（1﹣x2）0成立，

又∵ln（1﹣x2）＝ln（1﹣x）+ln（1+x），

∴，即[f（x）ln（1﹣x2）]′＞0恒成立，

可知函数g（x）＝f（x）ln（1﹣x2）在（0，1）上单调递增，

∵f（x）是奇函数，∴g（x）＝f（x）ln（1﹣x2）是奇函数，则在（﹣1，0）上单调递增，

又f（）＝f（）＝0，∴g（）＝f（）＝0，

∴g（x）的图象如下：

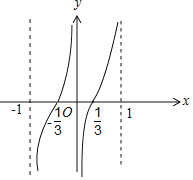
在（﹣1，），（0，）上，g（x）＜0，而ln（1﹣x2）＜0，∴f（x）＞0成立．

∴不等式f（x）＞0的解集为．

故选：B．