
分析 利用三角函数的平方关系式,结合换元法,通过二次函数的闭区间的最值求解即可.
解答 解:y=3-sinx-2cos2x=3-sinx-2(1-sin2x)=2sin2x-sinx+1.…(3分)
令sin x=t,x∈$[\frac{π}{6},\frac{7π}{6}]$,t∈[-$\frac{1}{2}$,1],…(6分)
则原函数可化为y=2t2-t+1,t∈[-$\frac{1}{2}$,1].…(8分)
当t=$\frac{1}{4}$时,ymin=$\frac{7}{8}$; …(10分)
当t=-$\frac{1}{2}$或t=1时,ymax=2.…(12分)
点评 本题考查三角函数的化简,三角函数的最值的求法,保护费以及二次函数的最值的求法,考查计算能力.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-1] | B. | [-3,-1] | C. | [1,+∞) | D. | (-∞,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{π}{2}]$ | B. | $[0,\frac{π}{3}],[\frac{5π}{6},π]$ | C. | $[\frac{π}{3},\frac{5π}{6}]$ | D. | $[\frac{π}{2},π]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
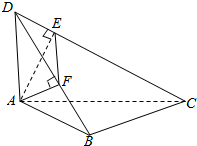 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com