
【题目】如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥底面ABC.已知D是BC的中点,AB=AA1=2.
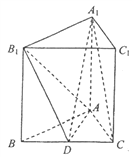
(I)求证:平面AB1D⊥平面BB1C1C;
(II)求证:A1C∥平面AB1D;
(III)求三棱锥A1-AB1D的体积.
【答案】(I)证明见解析;(II)证明见解析;(III)![]() .
.
【解析】试题分析:(1)利用线面垂直的判定定理,证得![]() 平面
平面![]() ,即可得出平面
,即可得出平面![]() 平面
平面![]() ;
;
(2)连接![]() ,设
,设![]() ,连接
,连接![]() ,由中位线定理可得
,由中位线定理可得![]() ,得到
,得到![]() 平面
平面![]() ;
;
(3)根据![]() ,即可求得三棱锥的体积.
,即可求得三棱锥的体积.
试题解析:
(I)证明:由已知△ABC为正三角形,且D是BC的中点,所以AD⊥BC.因为侧棱AA1⊥底面ABC,AA1∥BB1,所以BB1⊥底面ABC.又因为AD![]() 底面ABC,所以BB1⊥AD.而B1B
底面ABC,所以BB1⊥AD.而B1B![]() BC=B,所以AD⊥平面BB1C1C.因为AD
BC=B,所以AD⊥平面BB1C1C.因为AD![]() 平面AB1D,所以平面AB1D⊥平面BB1C1C.
平面AB1D,所以平面AB1D⊥平面BB1C1C.
(II)证明:连接A1B,设A1B![]() AB1=E,连接DE.
AB1=E,连接DE.
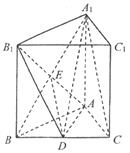
由已知得,四边形A1ABB1为正方形,则E为A1B的中点.
因为D是BC的中点,所以DE∥A1C.
又因为DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D,
平面AB1D,
所以A1C∥平面AB1D.
(III)由(II)可知A1C∥平面AB1D,所以A1与C到平面AB1D的距离相等,
所以![]() .由题设及AB=AA1=2,得BB1=2,且
.由题设及AB=AA1=2,得BB1=2,且![]() .
.
所以![]() =
=![]() ×
×![]() ,
,
所以三棱锥A1-AB1D的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() 均有
均有![]() 则称函数
则称函数![]() 具有性质
具有性质![]()
(Ⅰ)判断下面两个函数是否具有性质![]() 并说明理由.
并说明理由.
①![]() ②
②![]()
(Ⅱ)若函数![]() 具有性质
具有性质![]() ,且
,且![]()
求证:对任意![]() 有
有![]()
(Ⅲ)在(Ⅱ)的条件下,是否对任意![]() 均有
均有![]() 若成立,给出证明;若不成立,给出反例.
若成立,给出证明;若不成立,给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
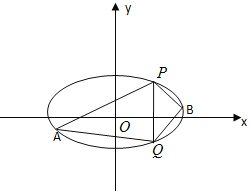
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的两条渐近线与抛物线
的两条渐近线与抛物线![]() 的准线分别交于A,B两点,O为坐标原点,若
的准线分别交于A,B两点,O为坐标原点,若![]() ,则双曲线的离心率
,则双曲线的离心率![]() __________.
__________.
【答案】![]()
【解析】因为双曲线![]() 的两条渐近线为
的两条渐近线为![]() ,抛物线
,抛物线![]() 的准线为
的准线为![]() ,所以
,所以![]() ,
,
因此![]()
点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
【题型】填空题
【结束】
16
【题目】若函数![]() 满足:对于
满足:对于![]() 图象上任意一点P,在其图象上总存在点
图象上任意一点P,在其图象上总存在点![]() ,使得
,使得![]() 成立,称函数
成立,称函数![]() 是“特殊对点函数”.给出下列五个函数:
是“特殊对点函数”.给出下列五个函数:
①![]() ;②
;②![]() (其中e为自然对数的底数);③
(其中e为自然对数的底数);③![]() ;④
;④![]() ;
;
⑤![]() .
.
其中是“特殊对点函数”的序号是__________.(写出所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆C:
分别是椭圆C: ![]() 的左、右焦点,其中右焦点为抛物线
的左、右焦点,其中右焦点为抛物线![]() 的焦点,点
的焦点,点 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)设与坐标轴不垂直的直线![]() 过
过![]() 与椭圆C交于A、B两点,过点
与椭圆C交于A、B两点,过点 且平行直线
且平行直线![]() 的直线交椭圆C于另一点N,若四边形MNBA为平行四边形,试问直线
的直线交椭圆C于另一点N,若四边形MNBA为平行四边形,试问直线![]() 是否存在?若存在,请求出
是否存在?若存在,请求出![]() 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A. 设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 若![]() 为真命题,则
为真命题,则![]() ,
, ![]() 中至少有一个为真命题
中至少有一个为真命题
C. 命题:“若![]() 是幂函数,则
是幂函数,则![]() 的图象不经过第四象限”的否命题是假命题
的图象不经过第四象限”的否命题是假命题
D. 命题“![]() ,
, ![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,
, ![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,且相邻的两个最值点的距离为
的部分图象如图所示,且相邻的两个最值点的距离为![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 的图象向左平移1个单位长度后得到函数
的图象向左平移1个单位长度后得到函数![]() 的图象,关于
的图象,关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com