
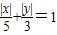 上的点,F1(-4,0),F2(4,0),则( )
上的点,F1(-4,0),F2(4,0),则( )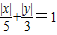 ,可以联想椭圆方程
,可以联想椭圆方程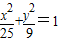 ,可知方程
,可知方程 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论 ,可以联想椭圆方程
,可以联想椭圆方程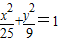 ,方程
,方程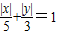 对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)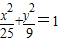 四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3) 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com