
【题目】设函数f(x)=tan(ωx+φ)(ω>0,0<φ<![]() ),已知函数y=f(x)的图象与x轴相邻两个交点的距离为
),已知函数y=f(x)的图象与x轴相邻两个交点的距离为![]() ,且图象关于点M(-
,且图象关于点M(-![]() ,0)对称.
,0)对称.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)求不等式-1≤f(x)≤![]() 的解集.
的解集.
科目:高中数学 来源: 题型:
【题目】在同一直角坐标系中,经过伸缩变换 后,曲线C的方程变为
后,曲线C的方程变为![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)过点![]() 作l的垂线l0交C于A,B两点,点A在x轴上方,求
作l的垂线l0交C于A,B两点,点A在x轴上方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .不过原点的直线
.不过原点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的值;
的值;
(2)若点![]() 在椭圆
在椭圆![]() 上,满足
上,满足![]() 的直线
的直线![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有![]() 成立.
成立.

(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个命题:
①如果向量![]() 与
与![]() 共线,则
共线,则![]() 或
或![]() ;
;
②![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③命题![]() :
:![]() ,
,![]() 的否定是
的否定是![]() :
:![]() ,
,![]() ;
;
④“指数函数![]() 是增函数,而
是增函数,而![]() 是指数函数,所以
是指数函数,所以![]() 是增函数”此三段论大前提错误,但推理形式是正确的.
是增函数”此三段论大前提错误,但推理形式是正确的.
以上命题正确的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 点测量到远处有一物体在做匀速直线运动,开始时该物体位于点
点测量到远处有一物体在做匀速直线运动,开始时该物体位于点![]() ,一分钟后,其位置在
,一分钟后,其位置在![]() 点,且
点,且![]() ,再过二分钟后,该物体位于
,再过二分钟后,该物体位于![]() 点,且
点,且![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.以上均不正确
D.以上均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
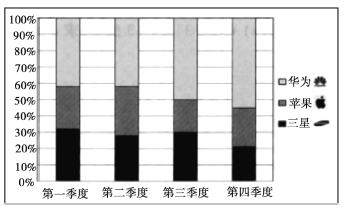
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com