练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗 (吨标准煤)的几组对照数据

    （1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

    (附: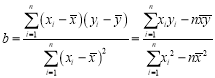，，，，其中,为样本平均值)

    【答案】（1）；（2）.

    【解析】

    （1）由表中数据和参考公式即求线性回归方程；

    （2）根据（1）中的线性回归方程进行预测，即得答案.

    （1）由表中数据可得.

    ，

    .

    所以线性回归方程为.

    （2）由（1）知线性回归方程为.

    把代入，得，

    所以生产100吨甲产品的生产能耗比技改前降低吨标准煤.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】（本小题满分16分）对于函数，如果存在实数使得，那么称为的生成函数．

    （1）下面给出两组函数，是否分别为的生成函数？并说明理由；

    第一组：；

    第二组：；

    （2）设，生成函数．若不等式在上有解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”：高铁、扫码支付、共享单车和网购．其中共享单车既响应绿色出行号召，节能减排，保护环境，又方便人们短距离出行，增强灵活性．某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车，三种车的计费标准均为每15分钟（不足15分钟按15分钟计）1元，按每日累计时长结算费用，例如某人某日共使用了24分钟，系统计时为30分钟．A同学统计了他1个月（按30天计）每天使用共享单车的时长如茎叶图所示，不考虑每月自然因素和社会因素的影响，用频率近似代替概率．设A同学每天消费元．

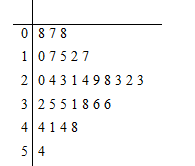
    （1）求的分布列及数学期望；

    （2）各品牌为推广用户使用，推出APP注册会员的优惠活动：红车月功能使用费8元，每天消费打5折；黄车月功能使用费20元，每天前15分钟免费，之后消费打8折；蓝车月功能使用费45元，每月使用22小时之内免费，超出部分按每15分钟1元计费．设分别为红车，黄车，蓝车的月消费，写出与的函数关系式，参考（1）的结果，A同学下个月选择其中一个注册会员，他选哪个费用最低？

    （3）该城市计划3个品牌的共享单车共3000辆正式投入使用，为节约居民开支，随机调查了100名用户一周的平均使用时长如下表：

    时长

    (0，15]

    (15，30]

    (30，45]

    (45，60]

    人数

    16

    45

    34

    5

    在（2）的活动条件下，每个品牌各应该投放多少辆？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法（修订草案）》中，提出推行生活垃圾分类制度，这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系，对某试点社区抽取户居民进行调查，得到如下的列联表.

    分类意识强

    分类意识弱

    合计

    试点后

    试点前

    合计

    已知在抽取的户居民中随机抽取户，抽到分类意识强的概率为.

    （1）请将上面的列联表补充完整；

    （2）判断是否有的把握认为居民分类意识的强弱与政府宣传普及工作有关？说明你的理由；

    参考公式：，其中.

    下面的临界值表仅供参考

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中表示不超过的最大整数，下列关于说法正确的有:______．

    ①的值域为[-1,1]

    ②为奇函数

    ③为周期函数，且最小正周期T=4

    ④在[0，2）上为单调增函数

    ⑤与的图像有且仅有两个公共点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某集团公司计划从甲分公司中的3位员工、、和乙分公司中的3位员工、、选择2位员工去国外工作.

    （1）若从这6名员工中任选2名，求这2名员工都是甲分公司的概率；

    （2）若从甲分公司和乙分公司中各任选1名员工，求这2名员工包括但不包括的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，抛物线，点，设直线与交于不同的两点、.

    （1）若直线轴，求直线的斜率的取值范围；

    （2）若直线不垂直于轴，且，证明：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    ①命题“2是素数且5是素数”是真命题

    ②命题“若x=y，则sinx=siny”的逆命题是真命题

    ③命题“x0∈R，x02﹣x0﹣2＞0”的否定是“x∈R，x2﹣x﹣2≤0”

    A. ①② B. ①③ C. ②③ D. ①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过曲线的左焦点作曲线的切线，设切点为，延长交曲线于点，其中有一个共同的焦点，若，则曲线的离心率为________．

    查看答案和解析>>

    同步练习册答案