
【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
【答案】(1)详见解析 (2) 90°
【解析】
试题分析:(1)证明四点共圆,一般利用对角互补进行证明:根据相切及垂径定理得OP⊥AP及OM⊥BC,从而得∠OPA+∠OMA=180°. (2)根据四点共圆得同弦所对角相等:∠OAM=∠OPM,因此
∠OPM+∠APM=90°,
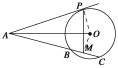
试题解析:(1)证明 连接OP,OM,因为AP与⊙O相切于点P,所以OP⊥AP.
因为M是⊙O的弦BC的中点,所以OM⊥BC,
于是∠OPA+∠OMA=180°.
由圆心O在∠PAC的内部,可知四边形APOM的对角互补,所以A、P、O、M四点共圆.
(2)解 由(1)得A、P、O、M四点共圆,
所以∠OAM=∠OPM,
由(1)得OP⊥AP,因为圆心O在∠PAC的内部,
所以∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.


科目:高中数学 来源: 题型:
【题目】中国象棋中规定:马走“日”字,象走“田”字.如下图,在中国象棋的半个棋盘(![]() 的矩形中每个小方格都是单位正方形)中,若马在
的矩形中每个小方格都是单位正方形)中,若马在![]() 处,可跳到
处,可跳到![]() 处,也可跳到
处,也可跳到![]() 处,用向量
处,用向量![]() ,
,![]() 表示马走了“一步”.通过探究,你能在图中画出马在
表示马走了“一步”.通过探究,你能在图中画出马在![]() 处走了一步的所有情况吗?
处走了一步的所有情况吗?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是__________.
①平均数![]() ; ②标准差
; ②标准差![]() ; ③平均数且标准差
; ③平均数且标准差![]() ;
;
④平均数![]() 且极差小于或等于2; ⑤众数等于1且极差小于或等于4.
且极差小于或等于2; ⑤众数等于1且极差小于或等于4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高一学生的数学与地理的水平测试成绩抽样统计如下表:若抽取的学生数为![]() ,成绩分为
,成绩分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)三个等级,设
(及格)三个等级,设![]() ,
, ![]() 分别表示数学成绩与地理成绩.例如:表中地理成绩为
分别表示数学成绩与地理成绩.例如:表中地理成绩为![]() 等级的共有
等级的共有![]() 人,数学成绩为
人,数学成绩为![]() 级且地理成绩为
级且地理成绩为![]() 等级的有8人.已知
等级的有8人.已知![]() 与
与![]() 均为
均为![]() 等级的频率是0.07.
等级的频率是0.07.
(1)设在该样本中,数学成绩优秀率是![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)已知![]() ,
, ![]() ,求数学成绩为
,求数学成绩为![]() 等级的人数比数学成绩为
等级的人数比数学成绩为![]() 等级的人数多的概率.
等级的人数多的概率.
人数
|
|
|
|
| 14 | 40 | 10 |
|
| 36 |
|
| 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列问题中符合调查问卷要求的是( )
A.你们单位有几个高个子?
B.您对我们厂生产的电视机满意吗?
C.您的体重是多少千克?
D.很多顾客都认为该产品的质量很好,您不这么认为吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com