
【题目】今天你低碳了吗?近来国内网站流行一种名为“碳排放计算器”的软件,人们可以由此计算出自己每天的碳排放量,如家居用电的碳排放量(千克)![]() 耗电度数
耗电度数![]() ,汽车的碳排放量(千克)
,汽车的碳排放量(千克)![]() 油耗公升数
油耗公升数![]() 等,某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这二族人数占各自小区总人数的比例
等,某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这二族人数占各自小区总人数的比例![]() 数据如下:
数据如下:
| 低碳族 | 非低碳族 |
| 低碳族 | 非低碳族 | |
比例 | 1/2 | 1/2 | 比例 | 4/5 | 1/5 |
(1)如果甲、乙来自![]() 小区,丙、丁来自
小区,丙、丁来自![]() 小区,求这4人中恰好有两人是低碳族的概率;
小区,求这4人中恰好有两人是低碳族的概率;
(2)![]() 小区经过大力宣传,每周非低碳中有20%的人加入到低碳族的行列,如果两周后随机地从
小区经过大力宣传,每周非低碳中有20%的人加入到低碳族的行列,如果两周后随机地从![]() 小区中任选5个人,记
小区中任选5个人,记![]() 表示5个人中的低碳族人数,求
表示5个人中的低碳族人数,求![]() 和
和![]()
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
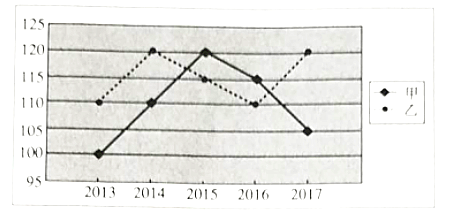
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: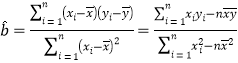 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织七匹三丈(1匹=![]() 尺,一丈=
尺,一丈=![]() 尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织
尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织![]() 尺,一月织了七匹三丈,问每天增加多少尺布?”若这一个月有
尺,一月织了七匹三丈,问每天增加多少尺布?”若这一个月有![]() 天,记该女子一个月中的第
天,记该女子一个月中的第![]() 天所织布的尺数为
天所织布的尺数为![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
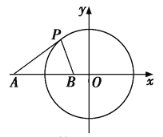
(1)求与直线l垂直,且与圆C相切的直线方程;
(2)在x轴上是否存在定点B(不同于点A),使得对于圆C上任一点P,![]() 为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求证:BF∥平面ADE;
(2)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1+ax+by)n的展开式中不含y的项的系数的绝对值的和为32,则a,n的值可能为( )
A.a=2,n=5B.a=1,n=6C.a=-1,n=5D.a=1,n=5
查看答案和解析>>
科目:高中数学 来源: 题型:
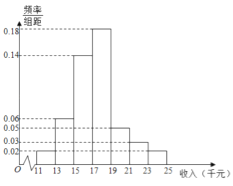
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民收入也逐年增加.为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图:
附:参考数据与公式 ![]() ,若
,若 ![]() ,则①
,则① ![]() ;②
;② ![]() ;③
;③ ![]() .
.
(1)根据频率分布直方图估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图可以认为该贫困地区农民年收入 X 服从正态分布 ![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() 近似为样本方差
近似为样本方差![]() ,经计算得:
,经计算得:![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每个农民的年收入相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用50元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com