
����Ŀ����ͼ��������ABCD��A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ������д��������ȷ����ı�ţ���
�ٵ�0��CQ�� ![]() ʱ��SΪ�ı���
ʱ��SΪ�ı���
�ڵ�CQ= ![]() ʱ��SΪ��������
ʱ��SΪ��������
�۵�CQ= ![]() ʱ��S��C1D1�Ľ���R����C1R=
ʱ��S��C1D1�Ľ���R����C1R= ![]()
�ܵ� ![]() ��CQ��1ʱ��SΪ������
��CQ��1ʱ��SΪ������
�ݵ�CQ=1ʱ��S�����Ϊ ![]() ��
��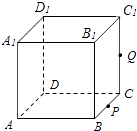
���𰸡��٢ڢۢ�
���������⣺��ͼ 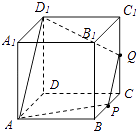
��CQ= ![]() ʱ����QΪCC1�е㣬��ʱ�ɵ�PQ��AD1 �� AP=QD1=
ʱ����QΪCC1�е㣬��ʱ�ɵ�PQ��AD1 �� AP=QD1= ![]() =
= ![]() ��
��
�ʿɵý���APQD1Ϊ�������Σ��ʢ���ȷ��
����ͼ����Q��C�ƶ�ʱ������0��CQ�� ![]() ��ֻ����DD1��ȡ��M����AM��PQ��
��ֻ����DD1��ȡ��M����AM��PQ��
���ɵý���Ϊ�ı���APQM���ʢ���ȷ��
�۵�CQ= ![]() ʱ����ͼ��
ʱ����ͼ��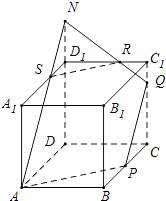
�ӳ�DD1��N��ʹD1N= ![]() ������AN��A1D1��S������NQ��C1D1��R������SR��
������AN��A1D1��S������NQ��C1D1��R������SR��
��֤AN��PQ���ɡ�NRD1�ס�QRC1 �� �ɵ�C1R��D1R=C1Q��D1N=1��2���ʿɵ�C1R= ![]() ������ȷ��
������ȷ��
���ɢۿ�֪�� ![]() ��CQ��1ʱ��ֻ���Q���Ƽ��ɣ���ʱ�Ľ�����״��Ȼ��ͼ��ʾ��APQRS����ȻΪ����Σ��ʴ���
��CQ��1ʱ��ֻ���Q���Ƽ��ɣ���ʱ�Ľ�����״��Ȼ��ͼ��ʾ��APQRS����ȻΪ����Σ��ʴ���
�ݵ�CQ=1ʱ��Q��C1�غϣ�ȡA1D1���е�F������AF����֤PC1��AF����PC1=AF��
��֪����ΪAPC1FΪ���Σ��������Ϊ ![]() AC1PF=
AC1PF= ![]() =
= ![]() ������ȷ��
������ȷ��
���Դ��ǣ��٢ڢۢݣ�
�����㾫�����������������ж���Ӧ���ǽ����ĸ�������Ҫ֪���������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() ��.
��.
��1���������![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ��
�� ![]() ��ֵ��
��ֵ��
��2����![]() ��
�� ![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ������������ֻ��һ������
������������ֻ��һ������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵�������� �̻��ع�Ч������
�̻��ع�Ч������![]() Խ��ʱ��ģ�͵����Ч��Խ���֮��Խ�ã��ڹ��������������һ�������������������������һ�㵽��������������ۺϷ�֤����ѧ�����ǡ�������������������֤����ѧ�����ǡ�ִ������������һ���ع鷽��
Խ��ʱ��ģ�͵����Ч��Խ���֮��Խ�ã��ڹ��������������һ�������������������������һ�㵽��������������ۺϷ�֤����ѧ�����ǡ�������������������֤����ѧ�����ǡ�ִ������������һ���ع鷽��![]() ������
������![]() ����1����λʱ��
����1����λʱ��![]() ƽ������5����λ�������Իع鷽��
ƽ������5����λ�������Իع鷽��![]() �ع���
�ع���![]() .���д���ĸ����У� ��
.���д���ĸ����У� ��
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ��˾�з�����һ���µ�����ʳƷ���Ӳ�Ʒ�г�ȡ100����Ϊ������������Щ��Ʒ��һ������ָ��ֵ���ɲ�������õ�����Ƶ�ʷֲ�ֱ��ͼ��

(1)��ֱ��ͼ��![]() ��ֵ��
��ֵ��
(2)����Ƶ�ʷֲ�ֱ��ͼ�����������ݵ���������λ�����Ƕ��٣����������������
(3)��Ƶ�ʷֲ�ֱ��ͼ������Ϊ�����ֲ�Ʒ������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ���Լ�����������
���Լ�����������![]() �ϵĸ���.
�ϵĸ���.
���ο����ݣ���![]() ����
����![]() ,
,![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֲ������ģ��ķ�������ij�˶�Ա���4�Σ����ٻ���3�εĸ��ʣ����ɼ���������0��9֮��ȡ����ֵ���������ָ��0,1��ʾû�л���Ŀ�꣬2,3,4,5,6,7,8,
9��ʾ����Ŀ�꣬��4�������Ϊһ�飬�������4�εĽ���������ģ�������20���������
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
�����������ݹ��Ƹ�����˶�Ա���4�����ٻ���3�εĸ���Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�������ɫѧУ�ķ�չ״����ij��������õ�����ͳ�����ݣ�
��� | 2014 | 2015 | 2016 | 2017 | 2018 |
��ɫѧУ | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
�������ϱ����ݣ�����![]() ��
��![]() �����ϵ��
�����ϵ��![]() ����˵��
����˵��![]() ��
��![]() �����������ǿ������֪��
�����������ǿ������֪��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��������Ժ�ǿ��
��������Ժ�ǿ��![]() ������Ϊ
������Ϊ![]() ��
��![]() ���������һ�㣻
���������һ�㣻![]() ������Ϊ
������Ϊ![]() ��
��![]() ��������Խ�������
��������Խ�������
������![]() ����
����![]() �����Իع鷽�̣���Ԥ������2019����ɫѧУ�ĸ�������ȷ��������
�����Իع鷽�̣���Ԥ������2019����ɫѧУ�ĸ�������ȷ��������
�ο���ʽ�� 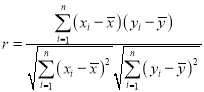 ��
��![]() ��
��![]() ��
��![]() ��
��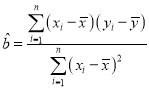 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ԲE�� ![]() �Ľ�����x����
�Ľ�����x����
��1������ԲE�Ľ���Ϊ1������ԲE�ķ��̣�
��2����F1 �� F2�ֱ�����ԲE�����ҽ��㣬PΪ��ԲE�ϵ�һ�����ڵĵ㣬ֱ��F2P��y���ڵ�Q������F1P��F1Q��֤������a�仯ʱ����P��ij��ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
������![]() ��������
��������![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() ������.
������.
����������![]() ����ͨ���̣���˵������ʾʲô���ߣ�
����ͨ���̣���˵������ʾʲô���ߣ�
����������![]() ��ֱ��
��ֱ��![]() �ֱ���
�ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ��
��![]() �ɵȱ����У���
�ɵȱ����У���![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com