
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
【答案】解:(Ⅰ)由f′(x)=kex﹣2x可知,
当k<0时,由于x∈(0,+∞),f′(x)=kex﹣2x<0,
故函数f(x)在区间(0,+∞)上是单调递减函数.
(Ⅱ)当k=2时,f(x)=2ex﹣x2,则f′(x)=2ex﹣2x,
令h(x)=2ex﹣2x,h′(x)=2ex﹣2,
由于x∈(0,+∞),故h′(x)=2ex﹣2>0,
于是h(x)=2ex﹣2x在(0,+∞)为增函数,
所以h(x)=2ex﹣2x>h(0)=2>0,即f′(x)=2ex﹣2x>0在(0,+∞)恒成立,
从而f(x)=2ex﹣x2在(0,+∞)为增函数,
故f(x)=2ex﹣x2>f(0)=2.
(Ⅲ)函数f(x)有两个极值点x1,x2,则x1,x2是f′(x)=kex﹣2x=0的两个根,
即方程 ![]() 有两个根,设
有两个根,设 ![]() ,则
,则 ![]() ,
,
当x<0时,φ′(x)>0,函数φ(x)单调递增且φ(x)<0;
当0<x<1时,φ′(x)>0,函数φ(x)单调递增且φ(x)>0;
当x>1时,φ′(x)<0,函数φ(x)单调递减且φ(x)>0.
要使 ![]() 有两个根,只需
有两个根,只需 ![]() .
.
故实数k的取值范围是 ![]() .
.
又由上可知函数f(x)的两个极值点x1,x2满足0<x1<1<x2,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
由于x1∈(0,1),故 ![]() ,
,
所以0<f(x1)<1.
【解析】(Ⅰ)求导数f′(x),由于f′(x)<0,即得f(x)在区间(0,+∞)上单调递减;(Ⅱ)根据导函数即可判断f(x)在(0,+∞)上的单调性,由单调性即可比较f(x)与2的大小;(Ⅲ)先求导数f′(x),由题意知x1、x2是方程f′(x)=0的两个根,令 ![]() ,利用导数得到函数φ(x)的单调区间,继而得到k的取值范围,由f′(x1)=0,则得
,利用导数得到函数φ(x)的单调区间,继而得到k的取值范围,由f′(x1)=0,则得 ![]() ,又由f(x1)=﹣(x1﹣1)2+1,x1∈(0,1),即可得到0<f(x1)<1.
,又由f(x1)=﹣(x1﹣1)2+1,x1∈(0,1),即可得到0<f(x1)<1.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值(极值反映的是函数在某一点附近的大小情况)的相关知识才是答题的关键.
在这个区间单调递减),还要掌握函数的极值(极值反映的是函数在某一点附近的大小情况)的相关知识才是答题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 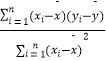 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
(1)求f(x)的解析式及单调递减区间;
(2)若存在x0∈[e,+∞),使函数g(x)=aelnx+ ![]() lnxf(x)≤a成立,求实数a的取值范围.
lnxf(x)≤a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点A(0,3)和B(6,0).
(Ⅰ)求线段AB垂直平分线的方程;
(Ⅱ)若曲线C上的任意一点P满足2|PA|=|PB|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=an+n2﹣1,数列{bn}满足3nbn+1=(n+1)an+1﹣nan , 且b1=3,a1=3.
(1)求数列{ an}和{bn}的通项an , bn;
(2)设Tn为数列{bn}的前n项和,求Tn , 并求满足Tn<7时n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且f(x+2)=f(x﹣2);当0≤x≤1时,f(x)= ![]() ,则f(1)+f(2)+f(3)+…+f等于( )
,则f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0 , f(x0)),其中x0满足f″(x0)=0.已知函数f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,则f(
,则f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的一个焦点与抛物线
的一个焦点与抛物线 ![]() 的焦点
的焦点 ![]() 重合,且点
重合,且点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,
, ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() .
.
(1)求椭圆 ![]() 的方程及点
的方程及点 ![]() 的坐标;
的坐标;
(2)过点 ![]() 的直线
的直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com