
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断
,判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(3)若![]() ,且
,且![]() 有三个不同实根,求
有三个不同实根,求![]() 的取值范围.
的取值范围.
【答案】(1)是奇函数;(2)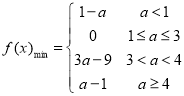 ;(3)
;(3)![]() .
.
【解析】
(1)由a=0,可得f(x)为奇函数,运用定义即可得到结论;
(2)求得f(x)的解析式,讨论a<1时,当1≤a≤3时,当3<a≤4时,当a>4时,结合单调性,可得最小值;
(3)由题意可得f(x)不单调,求得f(x)的分段函数,讨论当x≥a递增,且a≥0,x<a不单调,以及当x<a递增,且a<0,x≥a不单调,可得![]() 的范围,即可得到所求取值范围.
的范围,即可得到所求取值范围.
解:(1)a=0,可得f(x)=x|x|+bx为奇函数,
由定义域为R,f(﹣x)=﹣x|﹣x|﹣bx=﹣(x|x|+bx)=﹣f(x),
则f(x)为奇函数;
(2)b=0,可得f(x)=x|x﹣a|
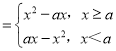 ,
,
由于1≤x≤3,
当a<1时,可得f(x)=x2﹣ax在[1,3]递增,
可得f(x)的最小值为f(1)=1﹣a;
当a>3时,f(x)=ax﹣x2在[1,![]() ]递增,(
]递增,(![]() ,3]递减,
,3]递减,
由f(1)﹣f(3)═a﹣1﹣(3a﹣9)=8﹣2a,
可得a>4时,f(1)<f(3),即为f(1)取得最小值a﹣1;
当3<a≤4时,f(1)≥f(3),可得f(3)取得最小值3a﹣9;
当1≤a≤3时,由f(x)≥0,可得x=a时,取得最小值0,
综上可得,a<1时,f(x)的最小值为1﹣a;
当1≤a≤3时,f(x)的最小值为0;
当3<a≤4时,f(x)的最小值为3a﹣9;
当a>4时,f(x)的最小值为a﹣1;
(3)b>0,且f(x)![]() 有三个不同实根,
有三个不同实根,
则f(x)不单调,
且f(x)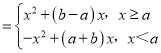 ,
,
当x≥a递增,且a≥0,x<a不单调,
可得![]() a,成立,又
a,成立,又![]() a,即a>b;
a,即a>b;
即ab![]() ,
,
即3ab<a2+b2<6ab,
则![]() 的取值范围是(
的取值范围是(![]() ,
,![]() );
);
当x<a递增,且a<0,x≥a不单调,
可得![]() a即a<﹣b,又
a即a<﹣b,又![]() a,即a≤b;
a,即a≤b;
即有![]() ab,不成立.
ab,不成立.
综上可得![]() 的取值范围是(
的取值范围是(![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() 是曲线
是曲线![]() 上但不在坐标轴上的任意一点,曲线
上但不在坐标轴上的任意一点,曲线![]() 与
与![]() 轴的焦点分别为
轴的焦点分别为![]() ,直线
,直线![]() 和
和![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,请问线段长之积
两点,请问线段长之积![]() 是否为定值?如果还请求出定值,如果不是请说明理由;
是否为定值?如果还请求出定值,如果不是请说明理由;
(3)在(2)的条件下,若点![]() 坐标为(-1,0),设过点
坐标为(-1,0),设过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的2个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各取2个球.
(1)求取出的4个球中恰有1个红球的概率;
(2)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),每一件产品的销售价格定为
万元(不含促销费用),每一件产品的销售价格定为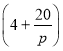 元,假定厂家的生产能力完全能满足市场的销售需求.
元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,某种算法(如下图所示)将报警时间划分为4段,分别为准备时间![]() 、人的反应时间
、人的反应时间![]() 、系统反应时间
、系统反应时间![]() 、制动时间
、制动时间![]() ,相应的距离分别为
,相应的距离分别为![]() 、
、![]() 、
、![]() 、
、![]() ,当车速为
,当车速为![]() (米/秒),且
(米/秒),且![]() 时,通过大数据统计分析得到下表(其中系数
时,通过大数据统计分析得到下表(其中系数![]() 随地面湿滑成都等路面情况而变化,
随地面湿滑成都等路面情况而变化,![]() ).
).
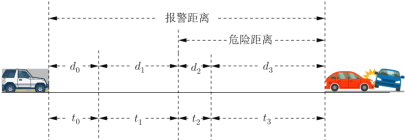
阶段 | 0、准备 | 1、人的反应 | 2、系统反应 | 3、制动 |
时间 |
|
|
|
|
距离 |
|
|
|
|
(1)请写出报警距离![]() (米)与车速
(米)与车速![]() (米/秒)之间的函数关系式
(米/秒)之间的函数关系式![]() ,并求
,并求![]() 时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间(精确到0.1秒);
时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间(精确到0.1秒);
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?合多少千米/小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com