
【题目】盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某款盲盒内可能装有某一套玩偶的![]() 、
、![]() 、
、![]() 三种样式,且每个盲盒只装一个.
三种样式,且每个盲盒只装一个.
(1)若每个盲盒装有![]() 、
、![]() 、
、![]() 三种样式玩偶的概率相同.某同学已经有了
三种样式玩偶的概率相同.某同学已经有了![]() 样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
(2)某销售网点为调查该款盲盒的受欢迎程度,随机发放了200份问卷,并全部收回.经统计,有![]() 的人购买了该款盲盒,在这些购买者当中,女生占
的人购买了该款盲盒,在这些购买者当中,女生占![]() ;而在未购买者当中,男生女生各占
;而在未购买者当中,男生女生各占![]() .请根据以上信息填写下表,并分析是否有
.请根据以上信息填写下表,并分析是否有![]() 的把握认为购买该款盲盒与性别有关?
的把握认为购买该款盲盒与性别有关?
女生 | 男生 | 总计 | |
购买 | |||
未购买 | |||
总计 |
参考公式: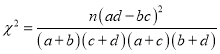 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)该销售网点已经售卖该款盲盒6周,并记录了销售情况,如下表:
周数 | 1 | 2 | 3 | 4 | 5 | 6 |
盒数 | 16 | ______ | 23 | 25 | 26 | 30 |
由于电脑故障,第二周数据现已丢失,该销售网点负责人决定用第4、5、6周的数据求线性回归方程,再用第1、3周数据进行检验.
①请用4、5、6周的数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(注: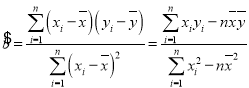 ,
,![]() )
)
②若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2盒,则认为得到的线性回归方程是可靠的,试问①中所得的线性回归方程是否可靠?
③如果通过②的检验得到的回归直线方程可靠,我们可以认为第2周卖出的盒数误差也不超过2盒,请你求出第2周卖出的盒数的可能取值;如果不可靠,请你设计一个估计第2周卖出的盒数的方案.
【答案】(1)![]() ;(2)表格见解析,有
;(2)表格见解析,有![]() 把握认为购买该款盲盒与性别有关;(3)①
把握认为购买该款盲盒与性别有关;(3)①![]() ;②是可靠的;③第2周卖出的盒数的可能值为18、19、20、21.
;②是可靠的;③第2周卖出的盒数的可能值为18、19、20、21.
【解析】
(1)用列举法写出所有基本事件,再从中找出满足要求的基本事件,用古典概型的公式即可求得结果;
(2)通过计算,完成列联表,再计算出观测值![]() ,比表中0.05所对应的数据3.841大,故得出结论“有
,比表中0.05所对应的数据3.841大,故得出结论“有![]() 把握认为购买该款盲盒与性别有关”;
把握认为购买该款盲盒与性别有关”;
(3)①将第4、5、6周的数据代入公式,计算出![]() 和
和![]() ,写出回归直线方程;
,写出回归直线方程;
②将第1、3周的数据代入①所求出的回归直线方程进行检验,该方程可靠;
③将![]() 代入①所求出的回归直线方程,解得
代入①所求出的回归直线方程,解得![]() ,根据可靠性的要求,以及该应用题的实际要求,得出第2周卖出的盒数的可能取值.
,根据可靠性的要求,以及该应用题的实际要求,得出第2周卖出的盒数的可能取值.
解:(1)由题意,基本事件空间为
![]() ,
,
其中基本事件的个数为9,
设事件![]() 为:“他恰好能收集齐这三种样式”,则
为:“他恰好能收集齐这三种样式”,则
![]() ,其中基本事件的个数为2,
,其中基本事件的个数为2,
则他恰好能收集齐这三种样式的概率![]() ;
;
(2)
女生 | 男生 | 总计 | |
购买 | 40 | 20 | 60 |
未购买 | 70 | 70 | 140 |
110 | 90 | 200 |
![]() ,
,
又因为![]() ,
,
故有![]() 把握认为“购买该款盲盒与性别有关”;
把握认为“购买该款盲盒与性别有关”;
(3)①由数据,求得![]() ,
,![]() ,
,
由公式求得
![]() ,
,
![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,
,
同样,当![]() 时,
时,![]() ,
,![]() ,
,
所以,所得到的线性回归方程是可靠的;
③由②可知回归直线方程可靠,
![]() 时
时![]() ,
,
设第二周卖出的盒数为![]() ,
,
则![]() ,
,
![]() ,
,
∴![]() 能取18、19、20、21,
能取18、19、20、21,
即第2周卖出的盒数的可能值为18、19、20、21.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如下茎叶图:
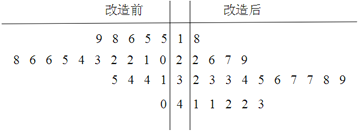
(Ⅰ)(1)设所采集的40个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
试写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根据(1)中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: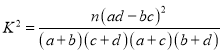 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天(
天(![]() )进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元
)进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元![]() 次;保障维护费第一次为0.2万元
次;保障维护费第一次为0.2万元![]() 周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() ,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 为两两不重合的平面,
为两两不重合的平面,![]() ,
,![]() ,
,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中真命题是( )
A.①③B.②④C.③④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
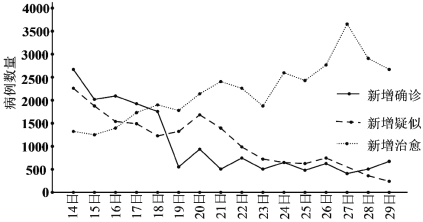
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数大于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于![]()
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶某村100户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标,将指标![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,得到如图所示的频率分布直方图.规定若
分成五组,得到如图所示的频率分布直方图.规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当![]() 时,认定该户为“亟待帮住户”.
时,认定该户为“亟待帮住户”.
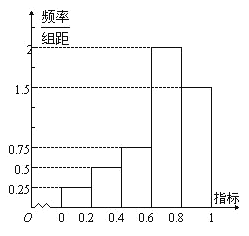
(1)为了更好的了解和帮助该村的这些贫困户,决定用分层抽样的方法从这100户中随机抽取20户进行更深入的调查,求应该抽取“绝对贫困户”的户数;
(2)从这20户中任取3户,求“绝对贫困户”多于“相对贫困户”的概率;
(3)现在从(1)中所抽取的“绝对贫困户”中任取3户,用![]() 表示所选3户中“亟待帮助户”的户数,求
表示所选3户中“亟待帮助户”的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com