
【题目】如下图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.

(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.
【答案】(1)见证明;(2)![]() (3)见解析
(3)见解析
【解析】
建立如图所示的空间直角坐标系,(1)通过证明![]() ,再结合
,再结合![]() 即可得结论;(2)结合(1)中的结论进一步说明
即可得结论;(2)结合(1)中的结论进一步说明![]() 是
是![]() 与平面
与平面![]() 所成的角,先通过向量夹角公式求出余弦值,再求正弦值;(3)由已知条件推导出
所成的角,先通过向量夹角公式求出余弦值,再求正弦值;(3)由已知条件推导出![]() 为二面角
为二面角![]() 的平面角,由此能推导出存在点
的平面角,由此能推导出存在点![]() 使得二面角
使得二面角![]() 是直二面角.
是直二面角.
以A为原点,![]() ,
,![]() 分别为y轴、z轴的正方向,
分别为y轴、z轴的正方向,
过A点且垂直于平面PAB的直线为x轴,建立空间直角坐标系![]() ,
,
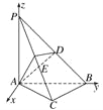
设PA=a,由已知可得:A(0,0,0),B(0,a,0),C![]() ,P(0,0,a).
,P(0,0,a).
(1)![]() =(0,0,a),
=(0,0,a),![]() =
=![]() ,∴
,∴![]() =0,∴
=0,∴![]() ⊥
⊥![]() ,∴BC⊥AP,
,∴BC⊥AP,
又∵∠BCA=90°,∴BC⊥AC,∴BC⊥平面PAC.
(2)∵D为PB的中点,DE∥BC,∴E为PC的中点,
∴D![]() ,E
,E![]() ,
,
∴由(1)知,BC⊥平面PAC,∴DE⊥平面PAC,垂足为点E,
∴∠DAE是AD与平面PAC所成的角,
∵![]() =
=![]() ,
,![]() =
=![]() ,∴cos∠DAE=
,∴cos∠DAE=![]() =
=![]() ,
,
∴AD与平面PAC所成的角的正弦值为![]() .
.
(3)∵DE∥BC,又由(1)知BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE平面PAC,PE平面PAC,
∴DE⊥AE,DE⊥PE,∴∠AEP为二面角A-DE-P的平面角.
∵PA⊥底面ABC,∴PA⊥AC,∴∠PAC=90°,
∴在棱PC上存在一点E,使得AE⊥PC,这时∠AEP=90°,
故存在点E,使得二面角A-DE-P是直二面角.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,直线
,直线![]()
![]() (
(![]() 为参数).
为参数).
(1)写出椭圆![]() 的参数方程及直线
的参数方程及直线![]() 的普通方程;
的普通方程;
(2)设![]() ,若椭圆
,若椭圆![]() 上的点
上的点![]() 满足到点
满足到点![]() 的距离与其到直线
的距离与其到直线![]() 的距离相等,求点
的距离相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程是
的参数方程是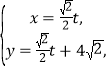 (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求圆心![]() 的直角坐标;
的直角坐标;
(Ⅱ)由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为平面直角坐标系
的顶点为平面直角坐标系![]() 的坐标原点
的坐标原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
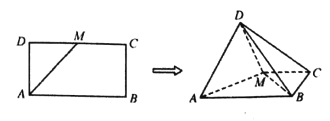
(1)当AB=2时,求三棱锥![]() 的体积;
的体积;
(2)求证:BM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且
的左、右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上任意一点,以
为椭圆上任意一点,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当圆
,当圆![]() 与直线
与直线![]() :
:![]() 有公共点时,求
有公共点时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com