
【题目】已知函数![]() ,对于任意的
,对于任意的![]()
![]() ,都有
,都有![]() , 当
, 当![]() 时,
时,![]() ,且
,且![]() .
.
( I ) 求![]() 的值;
的值;
(II) 当![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
(III) 设函数![]() ,判断函数g(x)最多有几个零点,并求出此时实数m的取值范围.
,判断函数g(x)最多有几个零点,并求出此时实数m的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)当
;(III)当![]() 时,函数
时,函数![]() 最多有
最多有![]() 个零点.
个零点.
【解析】
(Ⅰ)根据条件,取特殊值求解;
(Ⅱ)根据定义,判断函数的单调性,进而求出函数的最值;
(Ⅲ)根据定义,判断函数为奇函数,得出g(x)=f(x2﹣2|x|﹣m),令g(x)=0即f(x2﹣2|x|﹣m)=0=f(0),根据单调性可得 x2﹣2|x|﹣m=0,根据二次函数的性质可知最多有4个零点,且m∈(﹣1,0).
(I)令![]() 得
得![]() ,得
,得![]() .
.
令![]() 得
得![]() ,
,
令![]() 得
得![]()
(II)任取![]() 且
且![]() ,则
,则![]() ,
,
因为![]() ,即
,即![]() ,
,
令 ![]()
则![]() .
.
由已知![]() 时,
时,![]() 且
且![]() ,则
,则![]() ,
,
所以 ![]() ,
,![]() ,
,
所以函数![]() 在R上是减函数,
在R上是减函数,
故 ![]() 在
在![]() 单调递减.
单调递减.
所以![]() ,
,
又![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
,
故![]() .
.
(III) 令![]() 代入
代入![]() ,
,
得![]() ,
,
所以![]() ,故
,故![]() 为奇函数.
为奇函数.
∴![]()
=![]()
=![]()
![]() ,
,
令![]() ,即
,即![]() ,
,
因为函数![]() 在R上是减函数,
在R上是减函数,
所以![]() ,即
,即![]() ,
,
所以当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.


科目:高中数学 来源: 题型:
【题目】某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.观察图形,回答下列问题.
,其部分频率分布直方图如图所示.观察图形,回答下列问题.

(1)求成绩在![]() 的频率,并补全这个频率分布直方图:
的频率,并补全这个频率分布直方图:
(2)估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)
(3)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率.
的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
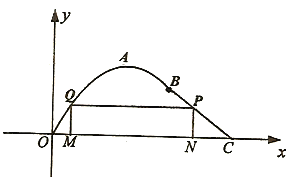
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:

①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象
的图象
B. 函数![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. 函数![]() 的图象关于
的图象关于![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内单调递增
内单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com