
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.
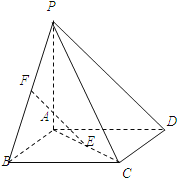
(1)证明:EF∥平面PCD;
(2)求证:面PBD⊥面PAC;
(3)若PA=AB,求PD与平面PAC所成角的大小.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a
1(a![]() b
b![]() 0)的左、右焦点分别为F1,F2,点P为椭圆C上不与左右顶点重合的动点,设I,G分别为△PF1F2的内心和重心.当直线IG的倾斜角不随着点P的运动而变化时,椭圆C的离心率为_____.
0)的左、右焦点分别为F1,F2,点P为椭圆C上不与左右顶点重合的动点,设I,G分别为△PF1F2的内心和重心.当直线IG的倾斜角不随着点P的运动而变化时,椭圆C的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
(1)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(2)为了研究新型冠状病毒的传染源和传播方式,从![]() 名确诊人员中随机抽出
名确诊人员中随机抽出![]() 人继续进行血清的研究,
人继续进行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 岁以下的人数,求
岁以下的人数,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: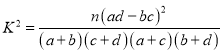 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆规是画椭圆的一种工具,如图1所示,在十字形滑槽上各有一个活动滑标![]() ,
,![]() ,有一根旋杆将两个滑标连成一体,
,有一根旋杆将两个滑标连成一体,![]() ,
,![]() 为旋杆上的一点,且在
为旋杆上的一点,且在![]() ,
,![]() 两点之间,且
两点之间,且![]() ,当滑标
,当滑标![]() 在滑槽
在滑槽![]() 内作往复运动,滑标
内作往复运动,滑标![]() 在滑槽
在滑槽![]() 内随之运动时,将笔尖放置于
内随之运动时,将笔尖放置于![]() 处可画出椭圆,记该椭圆为
处可画出椭圆,记该椭圆为![]() .如图2所示,设
.如图2所示,设![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 的左右顶点,点
的左右顶点,点![]() 为直线
为直线![]() 上的动点,直线
上的动点,直线![]() ,
,![]() 分别交椭圆于
分别交椭圆于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积为
面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com