
(13分)(2011•天津)编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
| | 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
| | 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 | [10,20) | [20,30) | [30,40] |
| 人数 | | | |
(Ⅰ)4,6,6
(Ⅱ)(i)(A3,A4),(A3,A5),(A3,A10),(A3,A11),(A3,A13),
(A4,A5),(A4,A10),(A4,A11),(A4,A13),(A5,A10),
(A5,A11),(A5,A13),(A10,A11),(A10,A13),(A11,A13)共15种
(ii)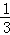
解析试题分析:(I)根据已知中编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录表,我们易得出得分在对应区间内的人数.
(II)(i)根据(I)的结论,我们易列出在区间[20,30)内的运动员中随机抽取2人,所有可能的抽取结果;
(ii)列出这2人得分之和大于50分的基本事件的个数,代入古典概型公式即可得到这2人得分之和大于50分的概率.
解:(I)由已知中编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录表易得:
得分在区间[10,20)上的共4人,在区间[20,30)上的共6人,在区间[30,40]上的共6人,
故答案为4,6,6
(II)(i)得分在区间[20,30)上的共6人,编号为A3,A4,A5,A10,A11,A13,
从中随机抽取2人,计为(X,Y),则所有可能的抽取结果有:
(A3,A4),(A3,A5),(A3,A10),(A3,A11),(A3,A13),
(A4,A5),(A4,A10),(A4,A11),(A4,A13),(A5,A10),
(A5,A11),(A5,A13),(A10,A11),(A10,A13),(A11,A13)共15种.
(ii)从得分在区间[20,30)内的运动员中随机抽取2人,这2人的得分之和大于50分的基本事件有:
(A4,A5),(A4,A10),(A4,A11),(A5,A10),(A10,A11)共5种
故这2人得分之和大于50分的概率P=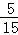 =
=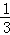
点评:本题主要考查用列举法计算随机事件所含的基本事件烽、古典概型及其概率计算公式等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力.


科目:高中数学 来源: 题型:解答题
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: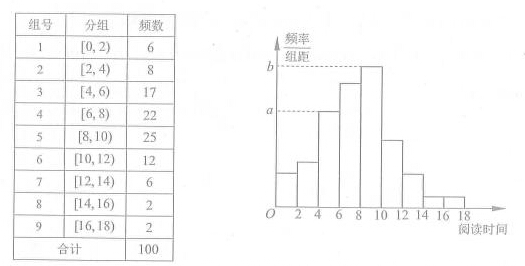
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组得到的频率分布表如下图所示,
| 班号 | 分组 | 频数 | 频率 |
| 第1组 | 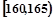 | 5 | 0.050 |
| 第2组 | 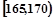 | ① | 0.350 |
| 第3组 | 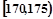 | 30 | ② |
| 第4组 | 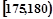 | 20 | 0.200 |
| 第5组 | 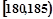 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容,成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人
(1)求该班考生中“阅读与表达”科目中成绩等级为A的人数;
(2)若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分,该考场中有2人10分,3人9分,从这5人中随机抽取2人,求2人成绩之和为19分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间加工零件的数量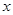 与加工时间
与加工时间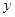 的统计数据如表:
的统计数据如表:
零件数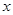 (个) (个) | 10 | 20 | 30 |
加工时间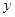 (分钟) (分钟) | 21 | 30 | 39 |
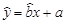 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学兴趣小组有男女生各 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
.
(1)求 ,
, 的值;
的值;
(2)现从成绩高于 分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了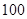 名年龄段在
名年龄段在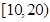 ,
,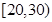 ,
, ,
,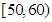 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
(1)求随机抽取的市民中年龄段在 的人数;
的人数;
(2)从不小于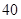 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取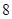 人,求
人,求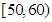 年龄段抽取的人数;
年龄段抽取的人数;
(3)从按(2)中方式得到的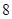 人中再抽取3人作为本次活动的获奖者,记
人中再抽取3人作为本次活动的获奖者,记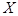 为年龄在
为年龄在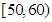 年龄段的人数,求
年龄段的人数,求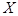 的分布列及数学期望.
的分布列及数学期望.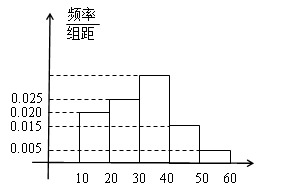
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市要建成宜商、宜居的国际化现代新城,该城市的东城区、西城区分别引进8甲厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com