【答案】
分析:(1)求出f′(x),利用导数判断f′(x)的单调性,由单调性即可求得其最小值;
(2)不妨设x
1≤x
2,构造函数K(x)=f(λ
1x+λ
2x
2)-λ
1f(x)-λ
2f(x
2)(x∈[0,x
2]),只需证明K(x)≤0,由(1)可判断K′(x)≥0,从而知函数K(x)在[0,x
2]上单调递增,故而K(x)≤K(x
2),得证;
(3)先证对任意的x
1,x
2,x
3∈[0,+∞)和实数λ
1≥0,λ
2≥0,λ
3≥0,且λ
1+λ
2+λ
3=1,总有f(λ
1x
1+λ
2x
2+λ
3x
3)≤λ
1f(x
1)+λ
2f(x
2)+λ
3f(x
3),运用(2)的结论容易证明,再令

,即可求得其最小值.
解答:(1)解:f′(x)=e
x-x,f''(x)=e
x-1
当x∈(-∞,0)时,f''(x)=e
x-1<0,即f′(x)在区间(-∞,0)上为减函数;
当x∈[0,+∞)时,f''(x)=e
x-1≥0,即f′(x)在区间[0,+∞)上为增函数;
于是f′(x)的最小值为f′(0)=1.
(2)证明:不妨设x
1≤x
2,构造函数K(x)=f(λ
1x+λ
2x
2)-λ
1f(x)-λ
2f(x
2)(x∈[0,x
2]),
则有K(x
2)=f(λ
1x
2+λ
2x
2)-λ
1f(x
2)-λ
2f(x
2)=0,
则

,
而λ
1x+λ
2x
2-x=(λ
1-1)x+λ
2x
2=λ
2(x
2-x)≥0,所以λ
1x+λ
2x
2≥x,
由(1)知f′(x)在区间[0,+∞)上为增函数,
所以

,即K′(x)≥0,
所以K(x)在[0,x
2]上单调递增,
所以K(x)≤K(x
2)=0,即f(λ
1x
1+λ
2x
2)≤λ
1f(x
1)+λ
2f(x
2).
(3)解:先证对任意的x
1,x
2,x
3∈[0,+∞)和实数λ
1≥0,λ
2≥0,λ
3≥0,且λ
1+λ
2+λ
3=1,
总有f(λ
1x
1+λ
2x
2+λ
3x
3)≤λ
1f(x
1)+λ
2f(x
2)+λ
3f(x
3),
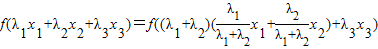
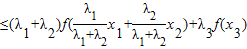

=λ
1f(x
1)+λ
2f(x
2)+λ
3f(x
3),
令
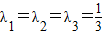
,有
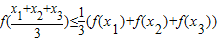
,
当x
1≥0,x
2≥0,x
3≥0且x
1+x
2+x
3=3时,有

.
所以f(x
1)+f(x
2)+f(x
3)的最小值为3e-

.
点评:本题考查利用导数研究函数的单调性、求函数的最值,考查学生综合运用知识分析问题解决问题的能力,考查学生对问题的转化能力,本题综合性强,难度大,能力要求高.

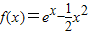 ,其导函数为f′(x).
,其导函数为f′(x). ,即可求得其最小值.
,即可求得其最小值. ,
, ,即K′(x)≥0,
,即K′(x)≥0,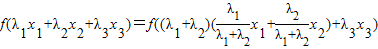
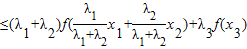

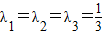 ,有
,有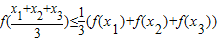 ,
, .
. .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 ,其导函数为
,其导函数为 .
.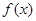 的单调减区间是
的单调减区间是 ;
;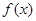 的极小值是
的极小值是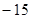 ;
; 时,对任意的
时,对任意的 且
且 ,恒有
,恒有
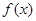 满足
满足
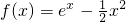 ,其导函数为f′(x).
,其导函数为f′(x).