【题目】如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．
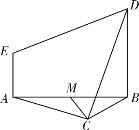
(1)证明：CM⊥DE；
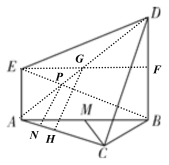
(2)在边AC上找一点N，使CD∥平面BEN.
【答案】（1）见解析；（2）
为
边上靠近
的三等分点；证明见解析.
【解析】
（1）根据等边三角形证得
，再根据面面垂直的性质定理得到线面垂直，利用线面垂直的性质得到结论；（2）取面
，当
与上一点连线构成平面时，根据线面平行性质定理可知：所得平面与面的交线必平行于
；两面已有一个交点
，则只需过作的平行线，与交点即为，根据长度关系可知：为边上靠近的三等分点；通过找
中点
得
，易证得
为
和
中点；根据平行线分线段成比例和长度关系可证得
，从而证得
，再利用三角形中位线得
，从而有
，根据线面平行判定定理，可证得结论成立.
（1）
为等边三角形，且
为
中点 
又平面
平面
，平面
平面
，
平面
平面
又
平面 
（2）为边上靠近的三等分点，证明如下：
取中点，连接交于
取中点
，连接；连接
交于
，为中点，
为中点
为边上靠近的三等分点
即
即
又
分别为
中点 
又
面
，
面 
面
快乐小博士巩固与提高系列答案科目：高中数学 来源： 题型：
【题目】已知函数f (x)＝ex，g(x)＝x－b，b∈R．
（1）若函数f (x)的图象与函数g(x)的图象相切，求b的值；
（2）设T(x)＝f (x)＋ag(x)，a∈R，求函数T(x)的单调增区间；
（3）设h(x)＝|g(x)|·f (x)，b＜1．若存在x1，x2
[0，1]，使|h(x1)－h(x2)|＞1成立，求b的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定椭圆C：
(a＞b＞0)，称圆C1：x2＋y2＝a2＋b2为椭圆C的“伴随圆”．已知椭圆C的离心率为
，且经过点(0，1)．
（1）求实数a，b的值；
（2）若过点P(0，m)(m＞0)的直线l与椭圆C有且只有一个公共点，且l被椭圆C的伴随圆C1所截得的弦长为2
，求实数m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙、丙3人投篮,投进的概率分别是
.
(Ⅰ)现3人各投篮1次,求3人都没有投进的概率；
(Ⅱ)用
表示乙投篮3次的进球数,求随机变量的概率分布及数学期望
；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】交通指数是指交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，记交通指数为
，其范围为
，分别有五个级别：
，畅通；
，基本畅通；
，轻度拥堵；
，中度拥堵；
，严重拥堵.在晚高峰时段（
），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示.
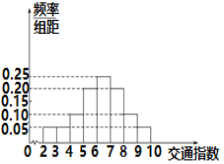
(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数；
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
(3)从(2)中抽取的6个路段中任取2个，求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区100位居民的人均月用水量(单位：
)的分组及各组的频数如下：
，4； 
，8； 
，15；
，22； 
，25； 
，14；
，6； 
，4； 
，2．
(1)列出样本的频率分布表；
(2)画出频率分布直方图，并根据直方图估计这组数据的平均数、中位数、众数；
(3)当地政府制定了人均月用水量为
的标准，若超出标准加倍收费，当地政府说，
以上的居民不超过这个标准，这个解释对吗？为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
