
【题目】如图所示,在直角坐标系![]() 中,曲线
中,曲线![]() 由中心在原点,焦点在
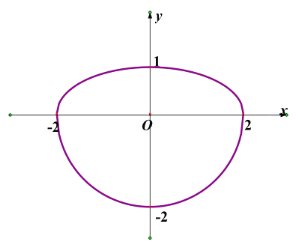
由中心在原点,焦点在![]() 轴上的半椭圆和以原点为圆心,半径为2的半圆构成,以坐标原点
轴上的半椭圆和以原点为圆心,半径为2的半圆构成,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 点,射线
点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解疫情期间哈一中高三学生的心理需求,更好的开展高考前的心理健康教育工作,心理老师设计了两个问题,第一个问题是“你出生的月份是奇数吗?”;第二个问题是“你是否需要心理疏导?”.让被调查者在保密的情况下掷一个均匀的骰子,其他人不知道掷骰子的结果,要求:当出现1点或2点时,回答第一个问题;否则回答第二个问题,由于其他人不知道他回答的是哪一个问题,因此,当他回答“是”时,你也无法知道他是否有心理问题,这种调查既保护了他的隐私,也能反映真实情况,可以从调查结果中得到需要的估计,若调查的900名学生中有156人回答“是”,由此可估计我校高三需要心理疏导的学生所占的比例约为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com