
【题目】已知椭圆![]() 的四个顶点围成的菱形的面积为
的四个顶点围成的菱形的面积为![]() ,椭圆的一个焦点为圆
,椭圆的一个焦点为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)若M,N为椭圆上的两个动点,直线OM,ON的斜率分别为![]() ,当
,当![]() 时,△MON的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
时,△MON的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作,它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图,执行该程序框图,求得该垛果子的总数![]() 为( )
为( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,依据图像可知,线段
的图像上任意不同的两点,依据图像可知,线段![]() 总是位于
总是位于![]() 两点之间函数图像的上方,因此有结论
两点之间函数图像的上方,因此有结论![]() 成立,运用类比的思想方法可知,若点
成立,运用类比的思想方法可知,若点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,则类似地有_________成立.
的图像上任意不同的两点,则类似地有_________成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起.设折起后点
折起.设折起后点![]() 的位置为
的位置为![]() ,并且平面
,并且平面![]()
![]() 平面
平面![]() .给出下面四个命题:
.给出下面四个命题:
①![]() ;②三棱锥
;②三棱锥![]() 的体积为
的体积为![]() ;③
;③![]()
![]() 平面
平面![]() ;
;
④平面![]() 平面
平面![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )


A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
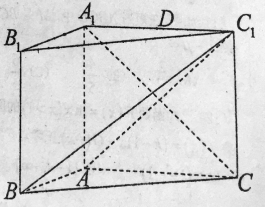
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求点
,若存在,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 为棱PC上一点.
为棱PC上一点.
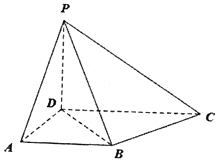
(Ⅰ)若点![]() 是PC的中点,证明:B
是PC的中点,证明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 试确定
试确定![]() 的值使得二面角
的值使得二面角![]() -BD-P为60°.
-BD-P为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长,设某地区城乡居民人民币储蓄存款![]() (单位:亿元)的数据如下:
(单位:亿元)的数据如下:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)2018年城乡居民储蓄存款前五名中,有三男和两女.现从这5人中随机选出2人参加某访谈节目,求选中的2人性别不同的概率.
附:回归直线的斜率和截距的最小二乘估计公式分别为:  ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com