
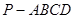 中,
中,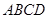 为平行四边形,且
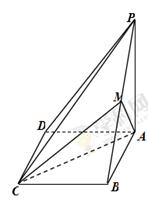
为平行四边形,且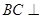 平面
平面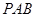 ,
,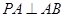 ,
,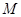 为
为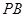 的中点,
的中点,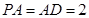 .
.
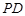 //
//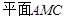 ;
;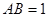 , 求二面角
, 求二面角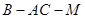 的余弦值.
的余弦值.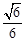 .
.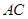 与
与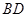 的交点
的交点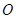 ,说明
,说明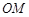 为
为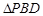 的中位线,
的中位线,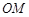 //
//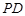 ,从而
,从而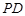 //
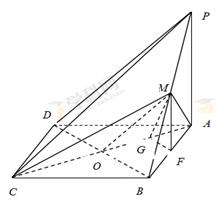
//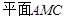 ;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点
;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点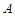 为坐标原点,分别以
为坐标原点,分别以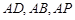 所在直线为
所在直线为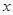 轴,
轴,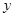 轴和
轴和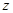 轴,建立空间直角坐标系
轴,建立空间直角坐标系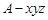 最佳,求平面
最佳,求平面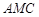 的法向量
的法向量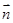 与平面
与平面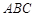 的一个法向量为
的一个法向量为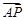 , 利用公式
, 利用公式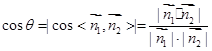 求解.
求解.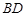 ,设
,设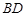 与
与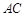 相交于点
相交于点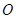 ,连接
,连接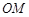 ,
,
 是平行四边形,∴点
是平行四边形,∴点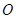 为
为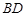 的中点.
的中点.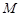 为
为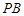 的中点,∴
的中点,∴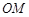 为
为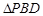 的中位线,
的中位线,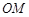 //
//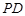 , 2分
, 2分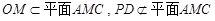 ,
,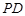 //
//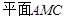 . 4分
. 4分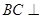 平面
平面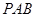 ,
,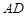 //
// , 则
, 则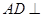 平面
平面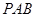 ,故
,故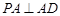 ,
,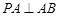 , 且
, 且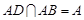 ,
,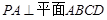 . 6分
. 6分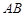 的中点
的中点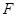 ,连接
,连接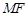 ,则
,则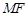 //
//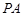 ,且
,且 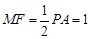 .
. 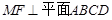 .
.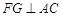 ,垂足为
,垂足为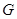 ,连接
,连接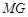 ,由于
,由于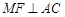 ,且
,且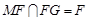 ,
,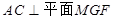 ,∴
,∴ 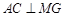 .
.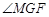 为二面角
为二面角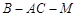 的平面角. 9分
的平面角. 9分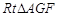 ∽
∽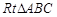 ,得
,得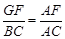 ,得
,得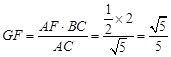 ,
,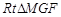 中,
中,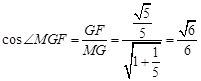 .
.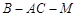 的余弦值为
的余弦值为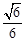 . 12分
. 12分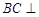 平面
平面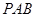 ,
,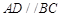 , 则
, 则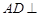 平面
平面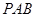 ,故
,故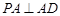 ,
,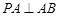 , 且
, 且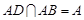 ,∴
,∴ . 6分
. 6分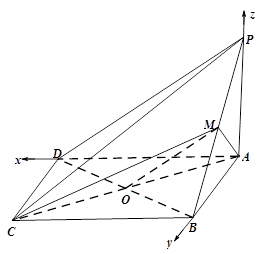
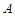 为坐标原点,分别以
为坐标原点,分别以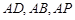 所在直线为
所在直线为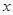 轴,
轴,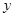 轴和
轴和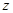 轴,建立空间直角坐标系
轴,建立空间直角坐标系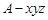 .则
.则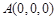 ,
,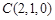 ,
,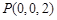 ,
,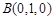 ,
,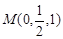 ,
, 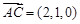 ,
, 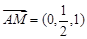 ,
,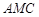 的法向量为
的法向量为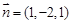 ,
, 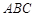 的一个法向量为
的一个法向量为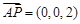 ,
, 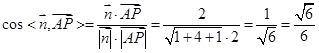 .
. 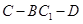 的余弦值为
的余弦值为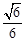 . 12分
. 12分

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源:不详 题型:单选题
| n1 |
| n2 |
| A.2 | B.-4 | C.-2 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
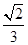 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.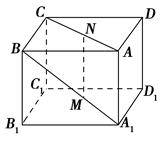
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.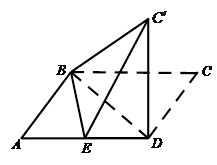
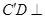 平面ABD;
平面ABD;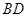 与平面
与平面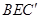 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
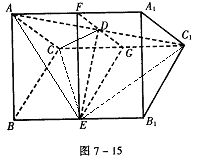
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com