
【题目】已知抛物线C:x2=2py(p>0)的焦点为F,直线l与抛物线C交于P,Q两点.
(1)若l过点F,抛物线C在点P处的切线与在点Q处的切线交于点G.证明:点G在定直线上.
(2)若p=2,点M在曲线y![]() 上,MP,MQ的中点均在抛物线C上,求△MPQ面积的取值范围.
上,MP,MQ的中点均在抛物线C上,求△MPQ面积的取值范围.
【答案】(1)证明见解析(2)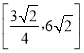
【解析】
(1)设![]() ,
,![]() ,根据条件分别求出直线PG的方程,QG的方程,联立可得
,根据条件分别求出直线PG的方程,QG的方程,联立可得![]() ,化简得到点G在定直线
,化简得到点G在定直线![]() 上.
上.
(2)设![]() ,表示出
,表示出![]() 的面积
的面积![]() .结合
.结合![]() 在曲线y
在曲线y![]() 上,即可求出面积的取值范围.
上,即可求出面积的取值范围.
(1)证明:易知![]() ,设
,设![]() ,
,![]() .
.
由题意可知直线l的斜率存在,故设其方程为![]() .
.
由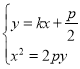 ,得
,得![]() ,所以
,所以![]() .
.
由![]() ,得
,得![]() ,
,![]() ,则
,则![]() ,
,
直线PG的方程为![]() ,即
,即![]() ①.
①.
同理可得直线QG的方程为![]() ②.
②.
联立①②,可得![]() .
.
因为![]() ,所以
,所以![]() ,故点G在定直线
,故点G在定直线![]() 上.
上.
(2)设![]() ,
,
![]() ,
,![]() 的中点分别为
的中点分别为 ,
,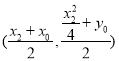 .
.
因为![]() ,
,![]() 得中点均在抛物线上,
得中点均在抛物线上,
所以![]() ,
,![]() 为方程
为方程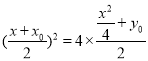 的解,
的解,
即方程![]() 的两个不同的实根,
的两个不同的实根,
则![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
所以![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,纵坐标为
,纵坐标为![]() .
.
则![]() ,
,
![]() ,
,
所以![]() 的面积
的面积![]() .
.
由![]() ,得
,得![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 面积的取值范围为
面积的取值范围为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若对任意的![]() ,有
,有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;
的最小值;
(3)记![]() ,
,![]() 为不超过
为不超过![]() 的最大整数,求
的最大整数,求![]() 的值.
的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
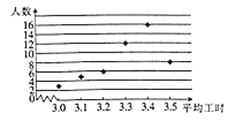
【题目】某工厂共有50位工人组装某种零件.下面的散点图反映了工人们组装每个零件所用的工时(单位:分钟)与人数的分布情况.由散点图可得,这50位工人组装每个零件所用工时的中位数为___________.若将500个要组装的零件分给每个工人,让他们同时开始组装,则至少要过_________分钟后,所有工人都完成组装任务.(本题第一空2分,第二空3分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,是以十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)形象化代表人的出生年份,现有十二生肖的吉祥物各一个,三位属相不同的小朋友依次每人选一个,则三位小朋友都不选和自己属相相同的吉祥物的选法有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
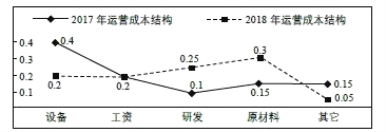
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com