
【题目】在△ABC中,内角A,B,C的对边分别是![]() ,向量
,向量![]() ,且
,且![]() .
.
(1)求角B的值;
(2)若![]() ,且
,且![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)![]() ;(2)△ABC的面积为
;(2)△ABC的面积为![]() 。
。
【解析】
(1)由向量数量积的坐标运算可将m·n=bcos B化为![]() cos C+
cos C+![]() cos A=bcos B,然后用正弦定理的结论边化角可得 sin Acos C+sin Ccos A=2sin Bcos B,进而再用两角和正弦公式和诱导公式可求cos B=
cos A=bcos B,然后用正弦定理的结论边化角可得 sin Acos C+sin Ccos A=2sin Bcos B,进而再用两角和正弦公式和诱导公式可求cos B=![]() ,进而可求角B。(2)由(1)知B=
,进而可求角B。(2)由(1)知B=![]() ,可将cos
,可将cos![]() =
=![]() sin A中的角C化为A,可得cos
sin A中的角C化为A,可得cos![]() =
=![]() sin A。利用两角差的余弦公式可得tan A=
sin A。利用两角差的余弦公式可得tan A=![]() ,求得A=
,求得A=![]() ,进而求得C=
,进而求得C=![]() .由|m|=
.由|m|=![]() 可得即a2+c2=20,在直角三角形中,可得a=
可得即a2+c2=20,在直角三角形中,可得a=![]() c,进而可求a,c的值。可求结论。
c,进而可求a,c的值。可求结论。
(1) 由m·n=bcos B,得![]() cos C+
cos C+![]() cos A=bcos B,
cos A=bcos B,
sin Acos C+sin Ccos A=2sin Bcos B,
即 sin(A+C)=2sin Bcos B,sin B=2sin Bcos B,
∵0<B<π,sin B≠0,
∴cos B=![]() ,
,
∴B=![]() .
.
(2) C=π-A-B=![]() -A,cos
-A,cos![]() =
=![]() sin A
sin A
∴cos![]() =
=![]() sin A
sin A
∴cos A=![]() sin Atan A=
sin Atan A=![]()
∵ 0<A<![]() π,
π,
∴A=![]() ,
,
∴C=π-![]() -
-![]() =
=![]() .
.
在Rt△ABC中,a=csin![]() =
=![]() c,
c,
又|m|=![]() ,即a2+c2=20,
,即a2+c2=20,
∴a=2,c=4,b=![]() =2
=2![]() ,
,
△ABC的面积S=![]() ×2×2
×2×2![]() =2
=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解某校高三毕业生报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图,已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
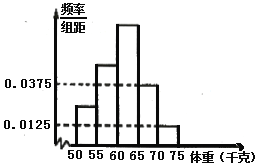
(Ⅰ)求该校报考体育专业学生的总人数![]() ;
;
(Ⅱ)已知A, ![]() 是该校报考体育专业的两名学生,A的体重小于55千克,
是该校报考体育专业的两名学生,A的体重小于55千克, ![]() 的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且
的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且![]() 在训练组的概率.
在训练组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作圆的切线
作圆的切线![]()
(1)当![]() 的横坐标为2时,求切线方程;
的横坐标为2时,求切线方程;
(2)求证:经过![]() 三点的圆
三点的圆![]() 必过定点,并求此定点的坐标;
必过定点,并求此定点的坐标;
(3)当线段![]() 长度最小时,求四边形
长度最小时,求四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象

A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移至![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S3=9,a1 , a3 , a7成等比数列.
(1)求数列{an}的通项公式;
(2)若an≠a1时,数列{bn}满足bn=2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
,![]() …,
…,![]() 分成9组,制成了如图所示的频率分布直方图。
分成9组,制成了如图所示的频率分布直方图。

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使82%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由。
的值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.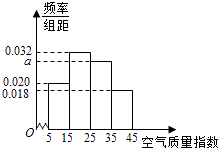
(1)求a的值;
(2)如果空气质量指数不超过15,就认定空气质量为“特优等级”,则从今年的监测数据中随机抽取3天的数值,其中达到“特优等级”的天数为X.求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com