【题目】椭圆
（
）的离心率是
，点
在短轴
上，且
。
（1）球椭圆
的方程；
（2）设
为坐标原点，过点
的动直线与椭圆交于
两点。是否存在常数
，使得
为定值？若存在，求
的值；若不存在，请说明理由。
【答案】（1）
；（2）见解析.
【解析】（Ⅰ）由已知，点C，D的坐标分别为（0，－b），（0，b）
又点P的坐标为（0，1），且
＝－1
于是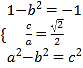
，解得a＝2，b＝
所以椭圆E方程为
.
（Ⅱ）当直线AB斜率存在时，设直线AB的方程为y＝kx＋1
A，B的坐标分别为（x1，y1），（x2，y2）
联立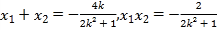
，得（2k2＋1）x2＋4kx－2＝0
其判别式△＝（4k）2＋8（2k2＋1）＞0
所以
从而
＝x1x2＋y1y2＋λ[x1x2＋（y1－1）（y2－1）]
＝（1＋λ）（1＋k2）x1x2＋k（x1＋x2）＋1
＝
＝－
所以，当λ＝1时，－＝－3
此时， 
＝－3为定值
当直线AB斜率不存在时，直线AB即为直线CD
此时
＝－2－1＝－3
故存在常数λ＝－1，使得
为定值－3.
科目：高中数学 来源： 题型：
【题目】供电部门对某社区1000位居民2017年12月份人均用电情况进行统计后，按人均用电量分为
五组，整理得到如下的频率分布直方图，则下列说法错误的是（ ）
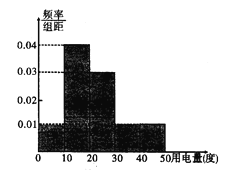
A. 12月份人均用电量人数最多的一组有400人
B. 12月份人均用电量不低于20度的有500人
C. 12月份人均用电量为25度
D. 在这1000位居民中任选1位协助收费，选到的居民用电量在
—组的概率为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】椭圆
的离心率是
，过点
的动直线
与椭圆相交于
两点，当直线
与
轴平行时，直线
被椭圆
截得的线段长为
.
（Ⅰ）求椭圆
的方程；
（Ⅱ）在
轴上是否存在异于点
的定点
，使得直线
变化时，总有
？若存在，求出点
的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】网格纸的各小格都是边长为1的正方形，图中粗实线画出的是一个几何体的三视图，其中正视图是正三角形，则该几何体的外接球表面积为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在等腰梯形
中， 
， 
， 
，四边形
为矩形，平面
平面
， 
.
（1）求证： 
平面
；
（2）点
在线段
上运动，设平面
与平面
所成二面角的平面角为
，试求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个正整数，若它的每个质因数都至少是两重的（即每个质因数乘方次数都不小于2），则称该正整数为“漂亮数”.相邻两个正整数皆为“漂亮数”，就称它们是一对“孪生漂亮数”.例如8与9就是一对“孪生漂亮数”.请你再找出两对“孪生漂亮数”来.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=|x+1|+|x﹣3|
（1）求函数f（x）的最小值；
（2）若{x|f（x）≤t2﹣3t}∩{x|﹣2≤x≤0}≠．求实数t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知F1 ， F2分别是椭圆 
的左、右焦点F1 ， F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点．
（1）求圆C的方程；
（2）设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a，b．当ab最大时，求直线l的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
