
分析 (1)先求出当α=$\frac{π}{4}$,直线L为:y=x-1,圆C:x2+y2=4,联立$\left\{\begin{array}{l}{y=x-1}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,得2x2-2x-3=0,利用韦达定理能求出直线L与圆C交点的中点坐标为($\frac{1}{2},-\frac{1}{2}$).
(2)直线L过定点P(1,0),圆C是圆心C(0,0),半径r=2的圆,由|PC|=1<2=r,能证明直线L与圆C相交.当相交弦与PC垂直时,相交弦最短.
解答 解:(1)∵直线L:$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),
∴$\frac{y}{x-1}$=tanα,
当α=$\frac{π}{4}$,直线L为:y=x-1,
∵圆C:$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),∴x2+y2=4,
∴圆C是圆心C(0,0),半径r=2的圆,
联立$\left\{\begin{array}{l}{y=x-1}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,得2x2-2x-3=0,
直线L与圆交于A(x1,y1),B(x2,y2),
则x1+x2=1,y1+y2=(x1-1)+(x2-1)=1-2=-1,
∴直线L与圆C交点的中点坐标为($\frac{1}{2},-\frac{1}{2}$).
证明:(2)∵直线L:$\frac{y}{x-1}$=tanα,∴直线L过定点P(1,0),
∵圆C是圆心C(0,0),半径r=2的圆,
∴|PC|=1,∵|PC|=1<2=r,
∴直线L与圆C相交.
当相交弦与PC垂直时,相交弦最短,
∴最短弦的长度dmin=2$\sqrt{{r}^{2}-|PC{|}^{2}}$=2$\sqrt{3}$.
点评 本题考查直线与圆相交弦中点坐标的求法,考查直线与圆垂直的证明,考查相交弦最短时其长度的求法,是中档题,解题时要认真审题,注意点到直线距离公式的合理运用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
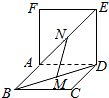 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
如图所示,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com