�����������������a
n=a
n+1-a
n=��n+1��
2-��n+1��-n
2+n=5n-4�����ԡ�a
n+1-��a
n=6���ɴ��ܹ�֤��{��a
n}�ǵȲ����У�
�����ɡ�
2 a
n-��a
n+1+a
n=-2
n��֪��a
n-a
n=2
n���ɴ������ܹ��������{a
n}��ͨ�ʽ���Ӷ�������{b
n}��ͨ�ʽ��
������a
n=n•2
n-1��c
n=
=
=
����n��2��n��N
*ʱ��
==(-)���Ӷ���֤��
����⣺���������⣺��a
n=a
n+1-a
n=3��n+1��
2-5��n+1��-3n
2+5n=6n-2����2�֣�
���a
n+1-��a
n=6
������{��a
n}������Ϊ4������Ϊ6�ĵȲ����У���3�֣�
�����ɡ�
2a
n-��a
n+1+a
n=-2
n�����a
n+1-��a
n-��a
n+1+a
n=-2
n��?��a
n-a
n=2
n��
����a
n=a
n+1-a
n����a
n+1-2a
n=2
n����5�֣�
��
-
=
����b
n+1-b
n=
����6�֣�
������{b
n}������
���
Ϊ����ĵȲ����У���b
n=
����7�֣�
�����ɣ���֪
=
����a
n=n•2
n-1��
��c=
=
=
��9�֣�
�൱n��2��n��N*ʱ
=
=
��
-
����
��c
1+
++
=1+
[��
-
��+��
-
��+��
-
��++��
-
��+��
-
��]
=1+
��
+
-
-
����1+
��
+
��=
��
��n=1ʱ��c
1=1��
����Ȼ����
��c
1+
++
��
����12�֣�
�������ڣ����⿼��Ȳ����е�֤��������ʱҪע��Ȳ��������ʵĺ������ã��ڣ����⿼������ͨ�ʽ����ⷽ��������ʱҪע��취�ĺ������ã��ڣ����⿼������ǰn��͵�֤��������ʱҪע��������ͷ��ĺ������ã�




 n2-
n2- n��n��N*������֤��{��an}�ǵȲ����У�
n��n��N*������֤��{��an}�ǵȲ����У�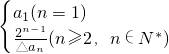 ����֤��b1+
����֤��b1+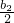 +��+
+��+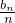 ��
��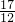 ��
��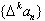 Ϊ{an}��k�ײ�����У�����
Ϊ{an}��k�ײ�����У�����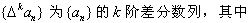
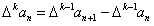 ����
����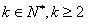 ��
��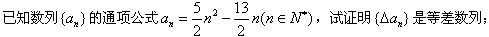
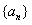 ������
������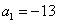 ��������
��������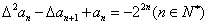 ��������
��������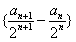 ��
��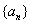 ��ͨ�ʽ��
��ͨ�ʽ�� 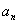 �Ƿ������Сֵ���������������Сֵ����������˵�����ɡ�
�Ƿ������Сֵ���������������Сֵ����������˵�����ɡ� 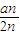 ��������{bn}��ͨ�ʽ��
��������{bn}��ͨ�ʽ�� ����֤��c1+
����֤��c1+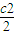 +��+
+��+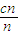 ��
��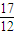 ��
��