练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．正三棱锥的顶点都在同一球面上．若该棱锥的高为3，底面边长为3，则该球的表面积为（　　）
    A．4πB．8πC．16πD．$\frac{32π}{3}$

    分析 设P-ABC的外接球心为O，则O在高PH上，延长AH交BC于D点，则D为BC中点，连接OA．等边三角形ABC中，求出AH=$\sqrt{3}$，然后在Rt△AOH中，根据勾股定理建立关于外接球半径R的方程并解之得R，用球的表面积公式可得P-ABC的外接球的表面积．

    解答 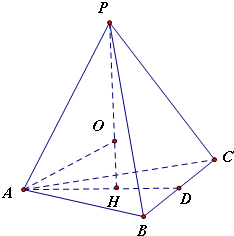解：设P-ABC的外接球球心为O，则O在高PH上，
    延长AH交BC于D点，则D为BC中点，连接OA，
    ∵等边三角形ABC中，H为中心，
    ∴AH=$\sqrt{3}$
    设外接球半径OA=R，则OH=3-R
    在Rt△AOH中，根据勾股定理得：OH2+AH2=OA2，
    即（3-R）2+3=R2，解之得R=2
    ∴P-ABC的外接球的表面积为：S=4πR2=16π
    故选C．

    点评 本题给出正三棱锥的底面边长和高，求它的外接球表面积，着重考查了正三棱锥的性质和球内接多面体等知识，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．若函数y=loga（x+1）（a＞0，a≠1）的图象过定点，则x值为（　　）
    A．-1B．0C．1D．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．假设关于某设备使用年限x和所支出的维修费用y（万元）有如下的统计资料：
    使用年限x23456
    维修费用y2.23.85.56.57.0
    若由资料知y对x呈线性相关关系．
    试求：（1）线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的回归系数$\stackrel{∧}{a}$，$\stackrel{∧}{b}$；
    （2）估计使用年限为10时，维修费用是多少？
    （参考公式）$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{a}=\stackrel{∧}{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$，其中$\overline{x}=\frac{1}{n}\sum_{i=1}^n{x_i}$，$\overline{y}=\frac{1}{n}\sum_{i=1}^n{y_i}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

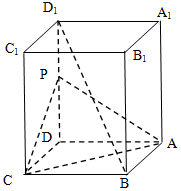    9．如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．
    （Ⅰ）求证：直线BD1∥平面PAC；
    （Ⅱ）求证：平面PAC⊥平面BDD1；
    （Ⅲ）求直线PB1与平面PAC所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．（Ⅰ）解不等式$\frac{{x}^{2}-x-6}{x-1}$＞0
    （Ⅱ）设a＞0，b＞0，c＞0，且a+b+c=1，求证（$\frac{1}{a}$-1）（$\frac{1}{b}$-1）（$\frac{1}{c}$-1）≥8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知直线的点斜式方程是$y-2=-\sqrt{3}（x-1）$，那么此直线的倾斜角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．函数?（x）=$\frac{1}{x+2}$的定义域是（-∞，-2）∪（-2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．如图，在四棱锥P-ABCD中，四边形ABCD是平行四边形，E、F分别是AB、PC中点，求证：EF∥面PAD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．如图，在四面体ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}=\overrightarrow b，\overrightarrow{AD}$=$\overrightarrow c$，点M在AB上，且AM=$\frac{2}{3}$AB，点N是CD的中点，则$\overrightarrow{MN}$=（　　）
    A．$\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$B．$-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$C．$\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow c$D．$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$

    查看答案和解析>>

    同步练习册答案