
【题目】已知抛物线![]() ,圆
,圆![]() ,圆心
,圆心![]() 到抛物线准线的距离为3,点
到抛物线准线的距离为3,点![]() 是抛物线在第一象限上的点,过点
是抛物线在第一象限上的点,过点![]() 作圆
作圆![]() 的两条切线,分别与
的两条切线,分别与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 18 | 7 | 25 |
女 | 12 | 13 | 25 |
合计 | 30 | 20 | 50 |
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设双曲线![]() 的上焦点为
的上焦点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为双曲线虚轴的左端点,已知
为双曲线虚轴的左端点,已知![]() 的离心率为
的离心率为![]() ,且
,且![]() 的面积
的面积![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)设抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() ,动直线
,动直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的准线相交于点
的准线相交于点![]() ,试推断以线段
,试推断以线段![]() 为直径的圆是否恒经过
为直径的圆是否恒经过![]() 轴上的某个定点
轴上的某个定点![]() ?若是,求出定点
?若是,求出定点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 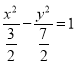
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上的截距相等,求此切线的方程.
轴上的截距相等,求此切线的方程.
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点为
向该圆引一条切线,切点为![]() ,
, ![]() 为坐标原点,且有
为坐标原点,且有![]() ,求使得
,求使得![]() 取得最小值的点
取得最小值的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com