
【题目】已知a<0,函数f(x)=acosx+ ![]() +
+ ![]() ,其中x∈[﹣
,其中x∈[﹣ ![]() ,
, ![]() ].
].
(1)设t= ![]() +
+ ![]() ,求t的取值范围,并把f(x)表示为t的函数g(t);
,求t的取值范围,并把f(x)表示为t的函数g(t);
(2)求函数f(x)的最大值(可以用a表示);
(3)若对区间[﹣ ![]() ,
, ![]() ]内的任意x1 , x2 , 总有|f(x1)﹣f(x2)|≤1,求实数a的取值范围.
]内的任意x1 , x2 , 总有|f(x1)﹣f(x2)|≤1,求实数a的取值范围.
【答案】
(1)解:∵ ![]() ,
,
又∵ ![]() ,∴cosx≥0,从而t2=2+2cosx,∴t2∈[2,4].
,∴cosx≥0,从而t2=2+2cosx,∴t2∈[2,4].
又∵t>0,∴ ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
, ![]()
(2)解:求函数f(x)的最大值即求 ![]() ,
, ![]() 的最大值.
的最大值.
![]() ,对称轴为
,对称轴为 ![]() .
.
当 ![]() ,即
,即 ![]() 时,
时, ![]() ;
;
当 ![]() ,即
,即 ![]() 时,
时, ![]() ;
;
当 ![]() ,即
,即 ![]() 时,gmax(t)=g(2)=a+2;
时,gmax(t)=g(2)=a+2;
综上可得,当 ![]() 时,f(x)的最大值是
时,f(x)的最大值是 ![]() ;当
;当 ![]() 时,f(x)的最大值是
时,f(x)的最大值是 ![]() ;
;
当 ![]() 时,f(x)的最大值是a+2
时,f(x)的最大值是a+2
(3)解:要使得|f(x1)﹣f(x2)|≤1对区间 ![]() 内的任意x1,x2恒成立,
内的任意x1,x2恒成立,
只需fmax(x)﹣fmin(x)≤1.也就是要求gmax(t)﹣gmin(t)≤1对 ![]() 成立
成立
∵当 ![]() ,即
,即 ![]() 时,gmin(t)=g(2)=a+2;
时,gmin(t)=g(2)=a+2;
且当 ![]() 时,
时, ![]()
结合问题(2)需分四种情况讨论:
① ![]() 时,
时, ![]() 成立,∴
成立,∴ ![]() ;
;
② ![]() 时,
时, ![]() ,即
,即 ![]() ,
,
注意到函数 ![]() 在
在 ![]() 上单调递减,故p(a)>p(
上单调递减,故p(a)>p( ![]() )=﹣
)=﹣ ![]() ,
,
于是 ![]() 成立,∴
成立,∴ ![]() ;
;
③ ![]() 时
时 ![]() ,即
,即 ![]() ,
,
注意到函数 ![]() 在
在 ![]() 上单调递增,
上单调递增,
故 ![]() ,于是
,于是 ![]() 成立,∴
成立,∴ ![]() ;
;
④ ![]() 时,
时, ![]() ,即
,即 ![]() ,∴
,∴ ![]() ;
;
综上,实数a的取值范围是 ![]()
【解析】(1)令 ![]() +
+ ![]() =t,换元可得;(2)问题转化为
=t,换元可得;(2)问题转化为 ![]() ,
, ![]() 的最大值,由二次函数分类讨论可得;(3)问题转化为gmax(t)﹣gmin(t)≤1对
的最大值,由二次函数分类讨论可得;(3)问题转化为gmax(t)﹣gmin(t)≤1对 ![]() 成立,分类讨论可得.
成立,分类讨论可得.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列几个命题:
① 命题![]() 任意
任意![]() ,都有
,都有![]() ,则
,则![]() 存在
存在![]() ,使得
,使得![]() .
.
② 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为假命题.
”的逆命题为假命题.
③ 空间任意一点![]() 和三点
和三点![]() ,则
,则![]() 是
是![]() 三点共线的充分不必要条件.
三点共线的充分不必要条件.
④ 线性回归方程![]() 对应的直线一定经过其样本数据点
对应的直线一定经过其样本数据点![]() 中的一个.
中的一个.
其中不正确的个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B分别是直线y=x和y=-x上的两个动点,线段AB的长为![]() ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,当|PQ|=3时,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧. 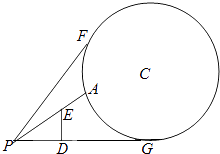
(1)若圆形标志物半径为25m,以PG所在直线为x轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即∠APF)的正切值为 ![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年电子商务蓬勃发展,在2017年的“年货节”期间,一网络购物平台推销了![]() 三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了
三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了![]() 三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对
三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对![]() 三种商品的抢购成功的概率分别为
三种商品的抢购成功的概率分别为![]() ,已知三件商品都被抢购成功的概率为
,已知三件商品都被抢购成功的概率为![]() ,至少有一件商品被抢购成功的概率为
,至少有一件商品被抢购成功的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若购物平台准备对抢购成功的![]() 三件商品进行优惠减免活动,
三件商品进行优惠减免活动, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项的和Sn,点(n,Sn)在函数
的前n项的和Sn,点(n,Sn)在函数![]() =2x2+4x图象上:
=2x2+4x图象上:
(1)证明![]() 是等差数列;
是等差数列;
(2)若函数![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() ,记cn=anbn,求数列
,记cn=anbn,求数列![]() 前n项和Tn;
前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=﹣x2+4x﹣![]() ≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sin2x+2+2cos2x.
sin2x+2+2cos2x.
(1)求f(x)的最小正周期与单调递减区间;
(2)在△ABC中,a,b,c分别是角A、B、C的对边,若f(A)=4,b=1,△ABC的面积为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是 ![]() ,则sin2θ﹣cos2θ的值等于( )
,则sin2θ﹣cos2θ的值等于( ) 
A.1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com