
分析 由已知条件求出直线l的普通方程为x+y-6=0,圆C的普通方程为x2+(y-2)2=4,由此能求出圆心到直线l的距离.
解答 解:∵在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=t+3}\\{y=3-t}\end{array}\right.$(参数t∈R),圆C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ+2}\end{array}\right.$,(参数θ∈[0,2π)),
∴直线l的普通方程为x-3=3-y,即x+y-6=0,
圆C的参数方程为$\left\{\begin{array}{l}{cosθ=\frac{x}{2}}\\{sinθ=\frac{y-2}{2}}\end{array}\right.$,(参数θ∈[0,2π)),
∴圆C的方程为x2+(y-2)2=4,圆心C(0,2),
∴圆心C(0,2)到直线l:x+y-6=0的距离:
d=$\frac{|0+2-6|}{\sqrt{{1}^{2}+{1}^{2}}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查圆心到直线的距离的求法,是基础题,解题时要认真审题,注意参数方程和普通方程的互化和点到直线的距离公式的合理运用.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
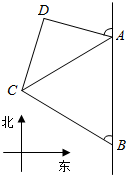 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
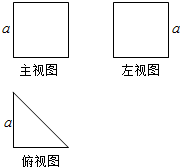 已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )
已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )| A. | (3+$\sqrt{2}$)a2 | B. | 4a2 | C. | (4+$\sqrt{2}$)a2 | D. | 3$\sqrt{2}$a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
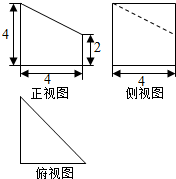
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com