
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 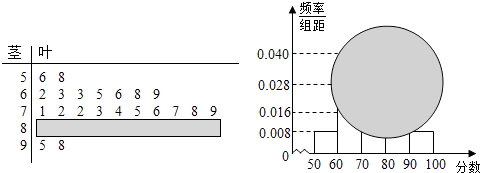
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
【答案】解:(Ⅰ)由频率分布直方图得分数在[50,60)的频率为0.008×10=0.08,
由茎叶图得分类在[50,60)的人数为2人,
∴全班人数为: ![]() =25人.
=25人.
(Ⅱ)由茎叶图得分数在[80,90)之间的频数为:
25﹣2﹣7﹣10﹣2=4人,
∵成绩为[80,90)间的频数为4,
∴频率分布直方图中[80,90)间的矩形的高为: ![]() =0.016.
=0.016.
(Ⅲ)由已知得X的可能取值为0,1,2,
由茎叶图知分数在良好以上有11人,其中分数为优秀有2人,
∴P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
E(X)= ![]() =
= ![]()
【解析】(Ⅰ)由频率分布直方图能求出分数在[50,60)的频率,由茎叶图得分类在[50,60)的人数,由此能求出全班人数.(Ⅱ)由茎叶图能求出分数在[80,90)之间的频数,由此能求出频率分布直方图中[80,90)间的矩形的高.(Ⅲ)由已知得X的可能取值为0,1,2,由茎叶图知分数在良好以上有11人,其中分数为优秀有2人,由此能求出X的分布列和E(X).
【考点精析】掌握频率分布直方图和离散型随机变量及其分布列是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°. 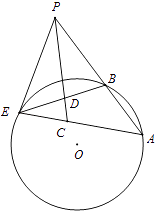
(1)求证: ![]()
(2)求∠PCE的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°. 
(1)求证: ![]()
(2)求∠PCE的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在城市旧城改造中,某小区为了升级居住环境,拟在小区的闲置地中规划一个面积为![]() 的矩形区域(如图所示),按规划要求:在矩形内的四周安排
的矩形区域(如图所示),按规划要求:在矩形内的四周安排![]() 宽的绿化,绿化造价为200元/
宽的绿化,绿化造价为200元/![]() ,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/
,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/![]() .设矩形的长为
.设矩形的长为![]() .
.
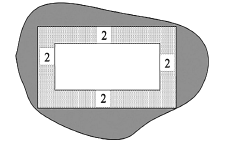
(1)设总造价![]() (元)表示为长度
(元)表示为长度![]() 的函数;
的函数;
(2)当![]() 取何值时,总造价最低,并求出最低总造价.
取何值时,总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图像相邻的两个对称中心之间的距离为
,其图像相邻的两个对称中心之间的距离为![]() ,且有一条对称轴为直线
,且有一条对称轴为直线![]() ,则下列判断正确的是 ( )
,则下列判断正确的是 ( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
D. 函数![]() 的图像关于点
的图像关于点![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com