
【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|![]() |的最小值的取值范围.
|的最小值的取值范围.
【答案】(1)x=1或3x+4y+5=0;(2)![]() <m<
<m<![]() ;(3)[
;(3)[![]() ,+∞)
,+∞)
【解析】
(1)当切线斜率不存在时,切线方程为x=1;当切线斜率存在时,设切线方程为y+2=k(x﹣1),由圆心到直线的距离等于半径求得k,则切线方程可求;
(2)由圆C1求得C1(m,2m),r1=2,再求得C2(0,0),r2=1,由圆C1与圆C2相交,得r1﹣r2<|C1C2|<r1+r2,由此可得实数m的范围;
(3)由题意![]() (﹣2,0)+(m﹣2,2m)
(﹣2,0)+(m﹣2,2m)![]() ,求得
,求得![]() 与
与![]() 共线时
共线时![]() 的范围为[1,3],而
的范围为[1,3],而![]() ,其最小值为
,其最小值为![]() ,由此可得当向量
,由此可得当向量![]() 与
与![]() 共线同向且
共线同向且![]() 与
与![]() 反向时,|
反向时,|![]() |的最小值最小,答案可求.
|的最小值最小,答案可求.
(1)当切线斜率不存在时,切线方程为x=1;
当切线斜率存在时,设切线方程为y+2=k(x-1),即kx-y-k-2=0.
由![]() ,解得k=-
,解得k=-![]() ,此时切线方程为3x+4y+5=0.
,此时切线方程为3x+4y+5=0.
∴切线方程为x=1或3x+4y+5=0;
(2)由圆C1:x2+y2-2mx-4my+5m2-4=0,得(x-m)2+(y-2m)2=4,
则C1(m,2m),r1=2,C2(0,0),r2=1.
由圆C1与圆C2相交,得r1-r2<|C1C2|<r1+r2,
∴1![]() ,即
,即![]() <m<
<m<![]() ;
;
(3)如图,O(0,0),C1(m,2m),P(2,0),
则![]() =
=![]() =(-2,0)+(m-2,2m)+
=(-2,0)+(m-2,2m)+![]()
=(m-4,2m)+![]() ,
,
∵![]() 与
与![]() 共线,∴
共线,∴![]() 的范围为[1,3],
的范围为[1,3],
而![]() =
=![]() ,
,
其最小值为![]() ,
,
∴当向量![]() 与
与![]() 共线同向且
共线同向且![]() 与
与![]() 反向时,|
反向时,|![]() |的最小值最小,为
|的最小值最小,为![]() ,
,
∴|![]() |的最小值的取值范围是[
|的最小值的取值范围是[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率
,离心率![]() .
.
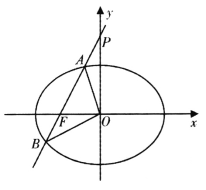
(I)求椭圆C的标准方程;
(II)已知直线![]() 交椭圆C于A,B两点.
交椭圆C于A,B两点.
①若直线![]() 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足![]() .求证:
.求证:![]() 为定值;
为定值;
②若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 与
与![]() 轴的左右交点分别为
轴的左右交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .
.
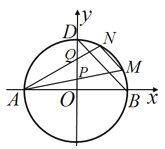
(1)若直线![]() 过点
过点![]() 并且与圆
并且与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,短轴端点到焦点的距离为
,短轴端点到焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为椭圆
为椭圆![]() 上任意两点,
上任意两点,![]() 为坐标原点,且
为坐标原点,且![]() .求证:原点
.求证:原点![]() 到直线
到直线![]() 的距离为定值,并求出该定值.
的距离为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.

(1)求进入决赛的人数;
(2)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在8.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com