解:(1)由条件①得f(0)=c=0,
由③f(-

+x)=f(-

-x)知f(x)的对称轴x=-

=-

,即a=b,
由②?x∈R,f(x)≥x,即ax
2+(a-1)x≥0,对?x∈R恒成立,
∴
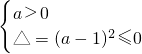
,
又(a-1)
2≥0,∴a=b=1,
∴f(x)=x
2+x.
(2)g(x)=f(x)-2x=x
2-x,其图象为开口向上的抛物线且对称轴为x=

,
所以g(x)在区间[-2,

]上单调递减,在区间[

,2]上单调递增;.
(3)存在实数t,使两函数图象恒有两个交点,理由如下:
h(x)=f(x)-x
2-x+t=t,
又函数u(x)=|log
2x|(x∈(0,2])在(0,1)上单调递减,在(1,2)上单调递增,又u(1)=0,u(2)=1,
∴h(x)与u(x)恒有两个不同交点得实数t的取值范围是(0,1].
分析:(1)由①f(0)=0可得c值,由③可知函数f(x)图象的对称轴方程,从而可得a,b间的关系式,由②可得f(x)-x≥0恒成立,根据恒成立问题可得一不等式,结合a,b间的关系即可求得a,b值;
(2)g(x)=f(x)-2x=x
2-x,结合其图象特征即可求得其单调区间;
(3)数形结合:h(x)=f(x)-x
2-x+t=t,结合u(x)的图象特征即可求得t的范围.
点评:本题主要考查了函数的解析式的求解,函数的单调区间,零点存在的判定定理,考查了分类讨论思想的在解题中的应用.属于综合性较强的试题.

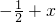 )=f(
)=f(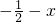 ).
). +x)=f(-
+x)=f(- -x)知f(x)的对称轴x=-
-x)知f(x)的对称轴x=- =-
=- ,即a=b,
,即a=b,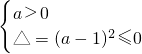 ,
, ,
, ]上单调递减,在区间[
]上单调递减,在区间[ ,2]上单调递增;.
,2]上单调递增;. 

 阅读快车系列答案
阅读快车系列答案