
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]()
【解析】试题分析:(1)将a=1代入求出函数的表达式,通过求导令导函数大于0,从而求出函数的单调递增区间;(2)问题转化为![]() 对1≤x≤e恒成立.记h(x)=
对1≤x≤e恒成立.记h(x)=![]() ,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
试题解析:
⑴![]() 时,
时, ![]() ,
, ![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
⑵由题意 ![]() 对
对![]() 恒成立,因为
恒成立,因为![]() 时,
时, ![]() , 所以
, 所以![]() 对
对![]() 恒成立.记
恒成立.记![]() ,因为
,因为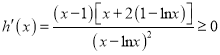 对
对![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,因此
,因此![]() .
.
⑶ 因为![]() ,由
,由![]() ,得
,得![]() 或
或![]() (舍).
(舍).
可证![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() ,
,
因为![]() ,所以
,所以![]() ,由于等号不能同时成立,所以
,由于等号不能同时成立,所以![]() ,于是
,于是![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数;
上是单调减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数.
上是单调增函数.
所以![]() ,
,
记![]() ,
, ![]() ,以下证明当
,以下证明当![]() 时,
时, ![]() .
.
![]() ,记
,记![]() ,
, ![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调减函数,
上单调减函数, ![]() ,
, ![]() ,所以
,所以![]() ,使
,使![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数;当
上是单调增函数;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数.又
上是单调减函数.又![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,所以
恒成立,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂在政府的帮扶下,准备转型生产一种特殊机器,生产需要投入固定成本![]() 万元,生产与销售均已百台计数,且每生产
万元,生产与销售均已百台计数,且每生产![]() 台,还需增加可变成本
台,还需增加可变成本![]() 万元,若市场对该产品的年需求量为
万元,若市场对该产品的年需求量为![]() 台,每生产
台,每生产![]() 百台的实际销售收入近似满足函数
百台的实际销售收入近似满足函数![]() .
.
(![]() )试写出第一年的销售利润
)试写出第一年的销售利润![]() (万元)关于年产量
(万元)关于年产量![]() (单位:百台,
(单位:百台,![]() ,
,![]() )的函数关系式:(说明:销售利润=实际销售收入-成本)
)的函数关系式:(说明:销售利润=实际销售收入-成本)
(![]() )因技术等原因,第一年的年生产量不能超过
)因技术等原因,第一年的年生产量不能超过![]() 台,若第一年的年支出费用
台,若第一年的年支出费用![]() (万元)与年产量
(万元)与年产量![]() (百台)的关系满足
(百台)的关系满足![]() ,问年产量
,问年产量![]() 为多少百台时,工厂所得纯利润最大?
为多少百台时,工厂所得纯利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,称
,称![]() 为
为![]() 的第
的第![]() 个坐标分量.若
个坐标分量.若![]() ,且满足如下两条性质:
,且满足如下两条性质:
①![]() 中元素个数不少于
中元素个数不少于![]() 个.
个.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 个坐标分量都是
个坐标分量都是![]() .则称
.则称![]() 为
为![]() 的一个好子集.
的一个好子集.
(![]() )若
)若![]() 为
为![]() 的一个好子集,且
的一个好子集,且![]() ,
,![]() ,写出
,写出![]() ,
,![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集,求证:
的一个好子集,求证:![]() 中元素个数不超过
中元素个数不超过![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集且
的一个好子集且![]() 中恰好有
中恰好有![]() 个元素,求证:一定存在唯一一个
个元素,求证:一定存在唯一一个![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 个坐标分量都是
个坐标分量都是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
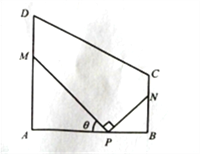
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, ![]() 百米,
百米, ![]() 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且![]() ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),![]() 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, ![]() 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设![]() .
.
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
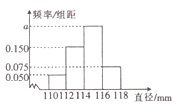
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
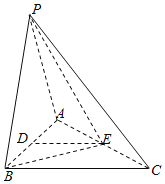
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求三棱锥P﹣BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
(1)估计这次考试成绩的众数,中位数,平均数;
(2)估计这次考试成绩的及格率(60分及其以上为及格).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com