Question

【题目】设等差数列{an}的公差d＞0，前n项和为Sn ， 已知3 是﹣a2与a9的等比中项，S10=﹣20．
（1）求数列{an}的通项公式；
（2）设bn= ，求数列{bn}的前n项和Tn（n≥6）．

Answer 1

【答案】
（1）解：∵3 是﹣a2与a9的等比中项，∴ =﹣a2a9，又S10=﹣20．

∴﹣（a1+d）（a1+8d）=45，10a1+ d=﹣20，

联立解得a1=﹣11，d=2．

∴an=﹣11+2（n﹣1）=2n﹣13

（2）解：1≤n≤5时，bn= = =﹣ ．

n≥6，bn= = = ，

∴n≥6时，数列{bn}的前n项和Tn=﹣ +

= ﹣

【解析】（1）利用等比数列的通项公式与性质、等差数列的通项公式与求和公式即可得出．（2）分类讨论，利用“裂项求和”方法即可得出．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系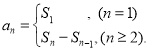；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．