
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).
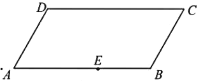
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
【答案】(1)![]() 是
是![]() 的中点;(2)
的中点;(2)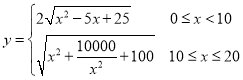 ;(3) 当
;(3) 当![]() ,
,![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.
【解析】
(1)由![]() 可知
可知![]() ,从而证明
,从而证明![]() 是
是![]() 的中点.
的中点.
(2)求出平行四边形的面积为![]() ,进而可求
,进而可求![]() ,从而用
,从而用![]() 可将
可将![]() 表示出来,利用余弦定理即可得到
表示出来,利用余弦定理即可得到![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当 ![]() ,由二次函数的性质可求最值;当
,由二次函数的性质可求最值;当![]() 时,由基本不等式可求最值.
时,由基本不等式可求最值.
解:(1)当点![]() 与点
与点![]() 重合时,由题设知,
重合时,由题设知,![]() .
.
于是![]() ,其中
,其中![]() 为平行四边形
为平行四边形![]() 边上的高.
边上的高.
得![]() ,即点
,即点![]() 是
是![]() 的中点.
的中点.
(2)因为点![]() 在线段
在线段![]() 上,所以
上,所以![]() .当
.当![]() 时,由(1)知
时,由(1)知
点![]() 在线段
在线段![]() 上.因为
上.因为![]()
所以![]() .
.
由![]() 得,
得,![]() .所以
.所以![]() 中,由余弦定理得
中,由余弦定理得
 .
.
当![]() 时,点
时,点![]() 在线段
在线段![]() 上,由
上,由![]()
得![]() .当
.当![]() 时,
时,![]()
当![]() 时,
时,![]()
化简均为![]() .
.
综上,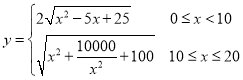 .
.
(3)当![]() 时,
时,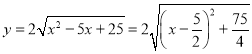 ,
,
于是当![]() 时,
时,![]() ,此时
,此时![]() .
.
当![]() 时,
时,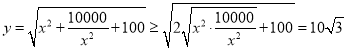
当且仅当![]() ,即
,即![]() 时,取等号
时,取等号
综上: 当![]() 距点
距点![]() ,
,![]() 距点
距点![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,以
的上、下顶点,以![]() 为直径作圆
为直径作圆![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() (
(![]() 为坐标原点)的面积;
为坐标原点)的面积;
(2)若点![]() 、
、![]() 分别在直线
分别在直线![]() 、
、![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
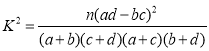 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
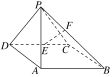
【题目】如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=![]() ,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
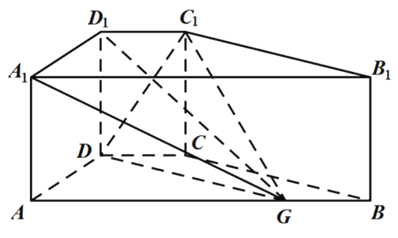
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB//CD,∠BAD=60°,CD=1,AD=2,AB=4,点G在线段AB上,AG=3GB,AA1=1
(1)证明:D1G/平面BB1C1C,
(2)求二面角A1-D1G-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种叫“对对碰”的游戏,游戏规则如下:一轮比赛中,甲乙两人依次轮流抛一枚质地均匀的硬币,甲先抛,每人抛3次,得分规则如下:甲第一次抛得![]() 分,再由乙第一次抛,若出现朝上的情况与甲第一次抛的朝上的情况一样,则本次得2分,否则得1分;再甲第二次抛,若出现朝上的情况与乙第一次抛的朝上的情况一样,则本次得分是乙第一次得分的基础上加1分,否则得1分;再乙第二次抛,若出现朝上的情况与甲第二次抛的朝上的情况一样,则本次得分是甲第二次得分的基础上加1分,否则得1分;按此规则,直到游戏结束.记甲乙累计得分分别为
分,再由乙第一次抛,若出现朝上的情况与甲第一次抛的朝上的情况一样,则本次得2分,否则得1分;再甲第二次抛,若出现朝上的情况与乙第一次抛的朝上的情况一样,则本次得分是乙第一次得分的基础上加1分,否则得1分;再乙第二次抛,若出现朝上的情况与甲第二次抛的朝上的情况一样,则本次得分是甲第二次得分的基础上加1分,否则得1分;按此规则,直到游戏结束.记甲乙累计得分分别为![]() .
.
(1)一轮游戏后,求![]() 的概率;
的概率;
(2)一轮游戏后,经计算得乙的数学期望![]() ,要使得甲的数学期望
,要使得甲的数学期望![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司生产新能源汽车,2019年3-9月份销售量(单位:万辆)数据如下表所示:
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
销售量 (万辆) | 3.008 | 2.401 | 2.189 | 2.656 | 1.665 | 1.672 | 1.368 |
(1)某企业响应国家号召,购买了6辆该公司生产的新能源汽车,其中四月份生产的4辆,五月份生产的2辆,6辆汽车随机地分配给A,B两个部门使用,其中A部门用车4辆,B部门用车2辆.现了解该汽车公司今年四月份生产的所有新能源汽车均存在安全隐患,需要召回.求该企业B部门2辆车中至多有1辆车被召回的概率;
(2)经分析可知,上述数据近似分布在一条直线附近.设![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,根据表中数据可计算出
,根据表中数据可计算出![]() ,试求出
,试求出![]() 的值,并估计该厂10月份的销售量.
的值,并估计该厂10月份的销售量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出1吨该蔬菜获利500元,未售出的蔬菜低价处理,每吨亏损100元.统计该蔬菜以往100个销售周期的市场需求量,绘制下图所示频率分布直方图.
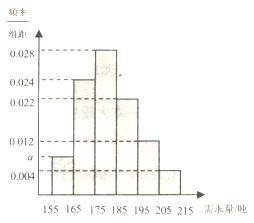
(Ⅰ)求![]() 的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
(Ⅱ)若经销商在下个销售周期购进了190吨该蔬菜,设![]() 为该销售周期的利润(单位:元),
为该销售周期的利润(单位:元),![]() 为该销售周期的市场需求量(单位:吨).求
为该销售周期的市场需求量(单位:吨).求![]() 与
与![]() 的函数解析式,并估计销售的利润不少于86000元的概率.
的函数解析式,并估计销售的利润不少于86000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com