Question

已知a是实数,函数f(x)=2ax²+2x-3-a.如果函数y=f(x)在区间［-1,1］上有零点,求a的取值范围.

(文)已知函数f(x)=x²+x-1,α、β是方程f(x)=0的两个根(α＞β),f′(x)是f(x)的导数.设a₁=1,a_n+1=a_n(n=1,2,…).

(1)求α、β的值;

(2)已知对任意的正整数n有a_n＞α,记b_n=ln(n=1,2,…),求数列{b_n}的前n项和S_n.

Answer 1

答案：分析:本小题主要考查二次函数及其性质、一元二次方程、函数应用、解不等式等基础知识,考查数形结合、函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识.

解：解法一:若a=0,则函数f(x)=2x-3在区间[-1,1]上没有零点.下面就a≠0时分三种情况讨论:

(1)方程f(x)=0在区间[-1,1]上有重根,此时Δ=4(2a²+6a+1)=0,解得a=.当a=时,f(x)=0的重根x=∈[-1,1];当a=时,f(x)=0的重根x=[-1,1].

故当方程f(x)=0在区间[-1,1]上有重根时,a=.

(2)f(x)在区间[-1,1]上只有一个零点且不是f(x)=0的重根.此时有f(-1)f(1)≤0.∵f(-1)=a-5,f(1)=a-1,∴(a-5)(a-1)≤01≤a≤5.∵当a=5时,方程f(x)=0在区间[-1,1]上有两个相异实根,故当方程f(x)=0在区间[-1,1]上只有一个根且不是重根时,1≤a＜5.

(3)方程f(x)=0在区间[-1,1]上有两个相异实根.∵函数f(x)=2a-(x+)²--a-3,

其图象的对称轴方程为x=-,a应满足:

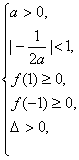(1)或(2)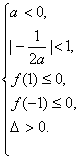

解不等式组(1)得a≥5.解不等式组(2)得a＜.

故当方程f(x)=0在区间[-1,1]上有两个相异实根时,a∈(-∞,)∪[5,+∞).

综上所述,函数y=f(x)在区间[-1,1]上有零点,则a的取值范围是(-∞,]∪[1,+∞).

解法二:若a=0,则函数f(x)=2x-3在区间[-1,1]上没有零点.

下面讨论a≠0时的情况:

(1)若f(-1)f(1)≤0,则f(x)必在[-1,1]上有零点.∵f(-1)=a-5,f(1)=a-1,∴(a-5)(a-1)≤01≤a≤5,即1≤a≤5时,函数f(x)在区间[-1,1]上有零点.

(2)若f(-1)f(1)＞0,下面分两种情况讨论:

①当f(-1)=a-5＞0,f(1)=a-1＞0,即a＞5时,

有|-|＜1,抛物线y=f(x)的对称轴x=-必在直线x=-1和x=1之间,且f(-)=--3-a＜0,于是f(-1)f(-)＜0,f(1)f(-)＜0.∴函数f(x)在区间(-1,-)和(-,1)内各有一个零点.

故当a＞5时,函数f(x)在区间[-1,1]上有零点.

②当f(-1)=a-5＜0,f(1)=a-1＜0,即a＜1时,

(ⅰ)当0＜a＜1时,f(x)=0的两根x₁,2=.

由于1+6a+2a²-(1+2a)²=2a(1-a)＞0,∴＞1+2a.

于是x₁=＞1,x₂=＜-1.

故当0＜a＜1时,函数f(x)在区间[-1,1]上没有零点.

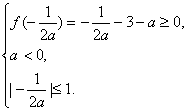(ⅱ)当a＜0时,若函数f(x)在区间[-1,1]上有零点,则f(x)的最大值f(-)≥0.否则由于f(-)是最大值,函数f(x)在区间[-1,1]上没有零点.此时抛物线y=f(x)的对称轴x=-在直线x=-1和x=1之间,即a满足解之,得a≤,

即当a≤时,函数f(x)在区间[-1,1]上有零点.

综上所述,若函数y=f(x)在区间[-1,1]上有零点,则a的取值范围是(-∞,]∪[1,+∞).

(文)分析:本小题主要考查函数、导数、一元二次方程、对数、数列等基础知识,考查合情推理、化归与转化、特殊与一般的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力.

解：(1)由x²+x-1=0解得方程的两根为x₁,2=.

又∵α、β是方程的两个根,且α＞β,∴α=,β=.

(2)∵f′(x)=2x+1,∴a_n+1=a_n-.

∵a_n＞α＞β(n=1,2,3,…),且a₁=1,∴b₁=ln=ln=lnβ⁴=4ln.

〔或b₁=ln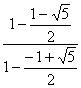=ln=ln=4ln〕

b_n+1=ln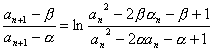

=2b_n,即{b_n}是以b₁为首项,以2为公比的等比数列.故数列{b_n}前n项之和为S_n==(2ⁿ-1)·4ln=(2ⁿ⁺²-4)ln.