
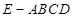 中,底面
中,底面 是正方形,
是正方形,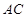 与
与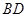 交于点
交于点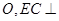 底面
底面 ,
,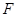 为
为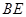 的中点.
的中点.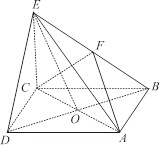
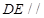 平面
平面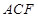 ;
;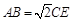 ,在线段
,在线段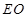 上是否存在点
上是否存在点 ,使
,使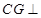 平面
平面 ?若存在,求出
?若存在,求出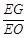 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 为线段
为线段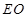 的中点时,
的中点时,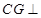 平面
平面 ,理由详见解析.
,理由详见解析.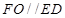 ,然后根据线面平行的判定定理进行证明即可;(2)这是存在性问题,先假设存在点
,然后根据线面平行的判定定理进行证明即可;(2)这是存在性问题,先假设存在点 ,使得
,使得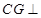 平面
平面 ,依据面面垂直的判定定理可知,这时必有面
,依据面面垂直的判定定理可知,这时必有面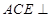 面
面 ,此时应该在平面
,此时应该在平面 中可以找到一条直线垂直平面
中可以找到一条直线垂直平面 ,这时关注好题目中的条件:底面
,这时关注好题目中的条件:底面 为正方形且
为正方形且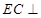 面
面 ,此时可想到可能是
,此时可想到可能是 面
面 ,这个垂直关系并不难证明,故可肯定点
,这个垂直关系并不难证明,故可肯定点 是存在的,然后再根据题中所给的条件去确定边
是存在的,然后再根据题中所给的条件去确定边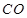 与
与 的比例关系,最后根据
的比例关系,最后根据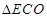 为直角三角形且
为直角三角形且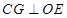 可确定
可确定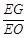 的比值.
的比值.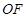
 是正方形可知,点
是正方形可知,点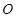 为
为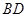 的中点
的中点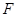 为
为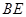 的中点,所以
的中点,所以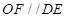
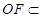 平面
平面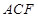 ,
,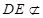 平面
平面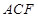
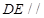 平面
平面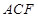 6分
6分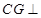 平面
平面 ,则必有
,则必有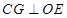
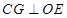 于点
于点
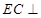 底面
底面 ,所以
,所以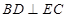 ,又底面
,又底面 是正方形
是正方形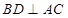 ,又
,又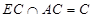 ,所以
,所以 平面
平面 10分
10分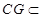 平面
平面 ,所以
,所以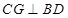
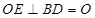 ,所以
,所以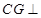 平面
平面 12分
12分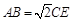 ,所以
,所以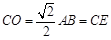
 为
为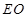 的中点,所以
的中点,所以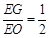 14分
14分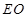 的中点
的中点 ,连接
,连接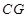 ,在四棱锥
,在四棱锥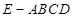 中
中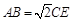 ,
,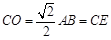 ,所以
,所以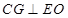 6分
6分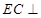 底面
底面 ,
,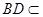 底面
底面 ,所以
,所以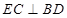
 是正方形可知,
是正方形可知,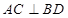
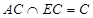
 平面
平面 10分
10分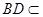 平面
平面
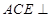 平面
平面 ,且平面
,且平面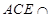 平面
平面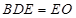
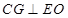 ,
,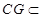 平面
平面 ,所以
,所以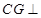 平面
平面 12分
12分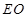 上存在点
上存在点 ,使
,使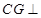 平面
平面
 为
为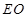 的中点,得
的中点,得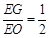 14分.
14分.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题

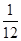 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①③ | B.②④ | C.①④ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 //平面
//平面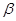 ,
,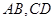 是夹在
是夹在 间的线段,若
间的线段,若 //
//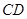 ,则
,则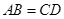 ;
; 是异面直线,
是异面直线,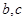 是异面直线,则
是异面直线,则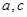 一定是异面直线;
一定是异面直线; //平面
//平面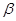 ,
,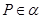 ,
, //
//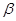 ,则
,则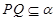 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 、
、 是不同的直线,
是不同的直线, 、
、 是不同的平面,则下列命题:
是不同的平面,则下列命题: ,则
,则 ;②若
;②若 ,则
,则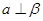 ;
; ,则
,则 ;④若
;④若 ,则
,则 .
.| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com