
【题目】已知![]() 为函数
为函数![]() 的导函数,且
的导函数,且![]() .
.
(1)判断函数![]() 的单调性;
的单调性;
(2)若![]() ,讨论函数
,讨论函数![]() 零点的个数.
零点的个数.
【答案】(1) ![]() 时,
时, ![]() 单调递减,
单调递减, ![]() 时,
时, ![]() 单调递增(2) 当
单调递增(2) 当![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 和
和![]() 或
或![]() 时,
时, ![]() 有两个零点,当
有两个零点,当![]() 且
且![]() ,
, ![]() 由三个零点.
由三个零点.
【解析】试题分析:(1)首先明确![]() 的表达式,求出
的表达式,求出![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,从而得到
,从而得到![]() 的单调区间;
的单调区间;
(2)由![]() ,得
,得![]() 或
或![]() ,若
,若![]() ,即
,即![]() ,
,
转而判断直线![]() 与
与![]() 的交点个数即可.
的交点个数即可.
试题解析:
(1)对![]() ,求导可得
,求导可得![]() ,
,
所以![]() ,与是
,与是![]() ,所以
,所以![]() ,
,
所以![]() ,
,
于是![]() 在
在![]() 上单调递增,注意到
上单调递增,注意到![]() ,
,
故![]() 时,
时, ![]() 单调递减,
单调递减, ![]() 时,
时, ![]() 单调递增.
单调递增.
(2)由(1)可知![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
若![]() ,则
,则![]() ,即
,即![]() ,
,
设![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
分析知![]() 时,
时, ![]() 时,
时, ![]() 时,
时, ![]() ,
,
现考虑特殊情况:
①若直线![]() 与
与![]() 相切,
相切,
设切点为![]() ,则
,则 ,整理得
,整理得![]() ,
,
设![]() ,显然
,显然![]() 在
在![]() 单调递增,
单调递增,
而![]() ,故
,故![]() ,此时
,此时![]() .
.

②若直线![]() 过点
过点![]() ,由
,由![]() ,则
,则![]() ,则
,则![]() ,
,
结合图形不难得到如下的结论:
当![]() 时,
时, ![]() 有一个零点;
有一个零点;
当![]() 和
和![]() 或
或![]() 时,
时, ![]() 有两个零点,
有两个零点,
当![]() 且
且![]() ,
, ![]() 由三个零点.
由三个零点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(Ⅰ)根据频率分布表中的数据,写出![]() ,
, ![]() 的值.
的值.
(Ⅱ)某人从灯泡样品中随机地购买了![]() 个,求
个,求![]() 个灯泡中恰有一个是优等品的概率.
个灯泡中恰有一个是优等品的概率.
(Ⅲ)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
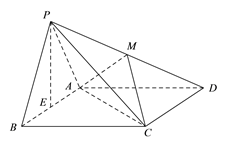
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2![]() +acos2
+acos2![]() =
=![]() c.
c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C=![]() ,△ABC的面积为2
,△ABC的面积为2![]() ,求c.
,求c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com