
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 为
为![]() 上两动点,且
上两动点,且![]() 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )

A.点![]() 到平面
到平面![]() 的距离B.直线
的距离B.直线![]() 与平面
与平面![]() 所成的角
所成的角
C.三棱锥![]() 的体积D.二面角
的体积D.二面角![]() 的大小
的大小
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: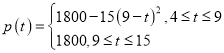 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为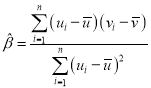 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东方商店欲购进某种食品(保质期两天),此商店每两天购进该食品一次(购进时,该食品为刚生产的).根据市场调查,该食品每份进价![]() 元,售价
元,售价![]() 元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区
元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区![]() 天的销售量如下表:
天的销售量如下表:

(视样本频率为概率)
(1)根据该产品![]() 天的销售量统计表,记两天中一共销售该食品份数为
天的销售量统计表,记两天中一共销售该食品份数为![]() ,求
,求![]() 的分布列与期望
的分布列与期望
(2)以两天内该产品所获得的利润期望为决策依据,东方商店一次性购进![]() 或
或![]() 份,哪一种得到的利润更大?
份,哪一种得到的利润更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上下顶点分别为
,上下顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为e.
,离心率为e.
(1)若![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,且
,且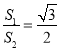 ,求椭圆C的方程;
,求椭圆C的方程;
(2)若![]() ,设直线
,设直线![]() 与椭圆C相交于P,Q两点,
与椭圆C相交于P,Q两点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,坐标原点O在以MN为直径的圆上,且
的中点,坐标原点O在以MN为直径的圆上,且![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com