
分析 如图所示,建立直角坐标系.$|{\overrightarrow e}|=1$,不妨设$\overrightarrow{e}$=(1,0),由$\overrightarrow a•\overrightarrow e=1$,$\overrightarrow b•\overrightarrow e=2$,不妨设$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,n),利用向量的模的计算即可求出$|{\overrightarrow a+\overrightarrow b}|$的最小值,再利用数量积运算即可得出$\overrightarrow a•\overrightarrow b$的最小值.
解答 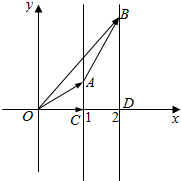 解:如图所示,建立直角坐标系.
解:如图所示,建立直角坐标系.
∵$|{\overrightarrow e}|=1$,不妨设$\overrightarrow{e}$=(1,0),
∵$\overrightarrow a•\overrightarrow e=1$,$\overrightarrow b•\overrightarrow e=2$,
不妨设$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,n).
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(3,m+n),
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=9+(m+n)2,
∴$|{\overrightarrow a+\overrightarrow b}|$的最小值为3,
∴$\overrightarrow{a}$-$\overrightarrow{b}$=(-1,m-n),
∵$|{\overrightarrow a-\overrightarrow b}|=2$,
∴1+(m-n)2=4,
∴(m+n)2=3+4mn≥0,
∴mn≥-$\frac{3}{4}$,当且仅当m=-n=±$\frac{\sqrt{3}}{2}$时取等号,
∴$\overrightarrow a•\overrightarrow b$=2+mn≥2-$\frac{5}{4}$=$\frac{5}{4}$.
故答案为:3,$\frac{5}{4}$
点评 本题考查了通过建立直角坐标系解决向量有关问题、数量积运算及其性质、不等式的性质,考查了推理能力和解决问题的能力,属于难题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?
某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com