若关于x的方程x2-x-a-1=0在区间x∈[-1,1]上有解,则a的取值范围是________.
[-

,1]
分析:先对关于x的二次方程在区间[-1,1]上有解分有一解和有两解两种情况讨论,当有一个解时,可以利用函数的零点的判定定理,再对每一种情况分别求对应的a的取值范围,最后综合即可.
解答:设f(x)=x
2-x-a-1,x∈[-1,1].
当△=0时,解得a=-

当△>0时,解得a>-

若f(x)=0在区间[-1,1]上有一个解.则f(-1)f(1)≤0,即(1-a)(-a-1)≤0,解得-1≤a≤1
当f(x)=0在区间[-1,1]上有两解,
则△>0,-1<-

<1,f(1)>0,f(-1)>0
∴1-4(-a-1)>0,1-a>0,-a-1>0
∴a>-

,a<1,a<-1
∴-
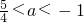
综上可知a的取值范围是[-

,1]
故答案为:[-

,1]
点评:本题考查了分类讨论的数学思想和一元二次方程根的分布与系数的关系,如果方程在某区间上有且只有一个根,可根据函数的零点存在定理进行解答,本题解题的关键是对于所给的条件的转化,在一个区间上有解,这里包含两种情况,这是题目的易错点,本题是一个中档题目.

 ,1]
,1]

 <1,f(1)>0,f(-1)>0
<1,f(1)>0,f(-1)>0 ,a<1,a<-1
,a<1,a<-1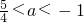
 ,1]
,1] ,1]
,1]
