
����Ŀ��ij������ȡ���������ַ�����ũ��ѡ��
����һ��ÿ��ÿ����ȡ������2Ԫ�����õ���������30��ʱ��ÿ��0.5Ԫ������30��ʱ���������ְ�ÿ��0.6Ԫ��ȡ��
�����������չ����ѣ�ÿ��0.58Ԫ��
��1����һ![]() �շѣ�Ԫ�����õ���
�շѣ�Ԫ�����õ���![]() ���ȣ���ĺ�����ϵ��
���ȣ���ĺ�����ϵ��
��2�������Ҿ��·ݰ�����һ����35Ԫ���������Ҹ����õ���ٶȣ�
��3�������Ҹ����õ�����ʲô��Χ�ڣ�ѡ��һ��ѡ�������ã�
���𰸡���1��![]() ��2�������Ҹ����õ�60�ȣ���3���������õ�����
��2�������Ҹ����õ�60�ȣ���3���������õ�����![]() ��Χ��ʱ��ѡ����һ�ȷ������ã�
��Χ��ʱ��ѡ����һ�ȷ������ã�
��������
���������1����![]() ��
��![]() ����������ۼ��ɣ�
����������ۼ��ɣ�
��2��ͨ���ֱ���![]() ��
��![]() ʱ
ʱ![]() ���㼴�ý��ۣ�
���㼴�ý��ۣ�
��3��ͨ���ֱ���![]() ��
��![]() ʱ
ʱ![]() ���㼴�ý��ۣ�
���㼴�ý��ۣ�
�����������1����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]()
��2����![]() ʱ����
ʱ����![]() ����
����![]() ����ȥ����
����ȥ����
��![]() ʱ��
ʱ��![]() ����
����![]() ��
��
���������Ҹ����õ�60�ȣ�
��3���跽�����շ�![]() ����
����![]() ��
��
��![]() ʱ����
ʱ����![]() ����
����![]() �����
�����![]() ����
����![]() ��
��
��![]() ʱ����
ʱ����![]() ����
����![]() �����
�����![]() ����
����![]() ��
��
���ϣ�![]() �����������õ�����
�����������õ�����![]() ��Χ��ʱ��ѡ����һ�ȷ������ã�
��Χ��ʱ��ѡ����һ�ȷ������ã�


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ����������![]() ��
��![]() ���ɣ�����
���ɣ�����![]() ����ԭ��
����ԭ��![]() Ϊ�е㣬
Ϊ�е㣬 ![]() Ϊ�������Բ��һ���֣�����
Ϊ�������Բ��һ���֣�����![]() ����
����![]() Ϊ���㣬
Ϊ���㣬 ![]() Ϊ����������ߵ�һ���֣�
Ϊ����������ߵ�һ���֣� ![]() ���������ߵ�һ������.
���������ߵ�һ������.
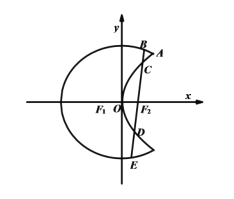
����������![]() ��
��![]() �ķ��̣�
�ķ��̣�
����![]() ��һ����
��һ����![]() ���ֱ��ֱ�ߣ��ֱ�������
���ֱ��ֱ�ߣ��ֱ�������![]() ���ν���
���ν���![]() �ĵ㣬��
�ĵ㣬��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬 ![]() Ϊ
Ϊ![]() ���е㣬�ʣ�
���е㣬�ʣ� ![]() �Ƿ�Ϊ��ֵ����������ö�ֵ��������˵������.
�Ƿ�Ϊ��ֵ����������ö�ֵ��������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����13��ҽ��������Ůҽ��6�ˣ��ִ��г��5��ҽ�����ҽ��С��ǰ����������ҽ��С��������2����ҽ����ͬʱ������3��Ůҽ�����費ͬ��ѡ�ɷ�������ΪN�������е�ʽ��
��C135��C71C64����C72C63+C73C62+C74C61+C75��
��C135��C71C64��C65�� ��C72C113��
�����ܳ�ΪN����ʽ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��������![]() �ļ�СֵΪ
�ļ�СֵΪ![]() ����
����![]() �����ֵ��
�����ֵ��
��������������ʵ��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ�ĸ�����( )
�����⡰x0��R��x��1��3x0���ķ��ǡ�x��R��x2��1��3x����
�ڡ�����f(x)��cos2ax��sin2ax����С������Ϊ�С��ǡ�a��1���ı�Ҫ�����������
��x2��2x��ax��x��[1,2]�Ϻ����(x2��2x)min��(ax)max��x��[1,2]�Ϻ������
�ܡ�ƽ������a��b�ļн��Ƕ۽ǡ��ij�Ҫ�����ǡ�a��b��0����
A��1 B��2
C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() .
.
��1����![]() ������
������![]() �ļ�Сֵ��
�ļ�Сֵ��
��2���躯��![]() ������
������![]() �ĵ������䣻
�ĵ������䣻
��3����������![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ��������
��������![]() ��ȡֵ��Χ����
��ȡֵ��Χ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڷ�ƶ��У�Ϊ�˾�����ƶ(��ծ��)�¸�����ҵ����Ӫ״�����õ�ij������Ʒר������5.8��Ԫ���Żݼ۸�ת�ø�������5��Ԫ��Ϣ����û�г�����С����ҵ�ң���Լ���Ӹõ꾭Ӫ�������У����ȱ�֤��ҵ�ҵ�ȫ��ְ��ÿ���������ѵĿ�֧3 600Ԫ������ת�÷�(����Ϣ)���ڼ��ṩ�������У�����������Ʒ�Ľ���Ϊÿ��14Ԫ���ڸõ�������Q(�ټ�)�������۸�P(Ԫ)�Ĺ�ϵ��ͼ��ʾ����ÿ������ֿ�֧2 000Ԫ��

(1)����Ʒ�ļ۸�Ϊÿ������Ԫʱ��������۳�ְ���������ѵ��������������
(2)��ҵ��ֻ�����õ꣬��������ڼ������ƶ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ������
������![]() .
.
��I����![]() �����ݼ����䣻
�����ݼ����䣻
��II����֪![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ڽ�
�ڽ�![]() �ĶԱߣ�
�ĶԱߣ�![]() Ϊ��ǣ�
Ϊ��ǣ�![]() ����
����![]() ǡ��
ǡ��![]() ��
��![]() �ϵ����ֵ����
�ϵ����ֵ����![]() ��
��![]() �����
�����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com