
【题目】某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
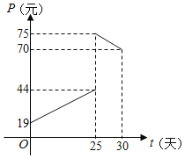
(1)请确定销售价格P(元)和时间t(天)的函数解析式;
(2)该商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)求该商品的日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
【答案】(1)![]() ;(2)
;(2)![]() ;
;
(3)第25天,日销售金额有最大值1125元.
【解析】
(1)根据已知中的图象可得函数是一个分段函数,分0≤t<25和25≤t≤30,t∈N两种情况,利用待定系数法可分别求出两段的解析式,最后综合讨论结果可得答案;(2)根据商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),结合(1)中销售价格P(元)和时间t(天)的函数解析式,根据:日销售金额=销售价格×销售量得到答案;(3)根据(2)中函数的解析式,结合二次函数的图象和性质,求出函数的最大值点及最大值,可得答案.
(1)当0≤t<25,t∈N,设P=at+b,将(0,19),(25,44)代入得![]() ,解之得
,解之得![]() ,∴P=t+19(0≤t<25,t∈N),当25≤t≤30,t∈N,同理可得P=﹣t+100,
,∴P=t+19(0≤t<25,t∈N),当25≤t≤30,t∈N,同理可得P=﹣t+100,
综上所述:销售价格P(元)和时间t(天)的函数解析式为![]() .
.
(2)由题意得,y=PQ,由(1)得![]() ,
,
即:![]() .
.
(3)由![]() ,
,
当0≤t<25,t∈N,由二次函数的图象和性质知t=10,或t=11时,y取最大值870元
当25≤t≤30,t∈N,由二次函数的图象和性质知t=25时,y取最大值1125元
综上所述,在第25天,日销售金额有最大值1125元


科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=8x的焦点为F,过点F作直线l与抛物线分别交于A,B两点,若点M满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求证:AC是∠DAB的平分线;
(2)求证:OF∥AG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的焦点为
)的焦点为![]() ,已知点
,已知点![]() ,
, ![]() 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足![]() .过弦
.过弦![]() 的中点
的中点![]() 作抛物线准线的垂线
作抛物线准线的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
【答案】1
【解析】设![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 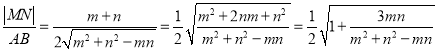
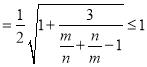 故最大值为1.
故最大值为1.
故答案为:1.
点睛:本题主要考查了抛物线的简单性质.解题的关键是利用了抛物线的定义。一般和抛物线有关的小题,很多时可以应用结论来处理的;平时练习时应多注意抛物线的结论的总结和应用。尤其和焦半径联系的题目,一般都和定义有关,实现点点距和点线距的转化。
【题型】填空题
【结束】
17
【题目】设![]() 的内角
的内角![]() ,
, ![]() ,
, ![]() 所对的边分别为
所对的边分别为![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com