
【题目】某同学在研究函数![]() 时,给出下面几个结论:
时,给出下面几个结论:
①等式![]() 对
对![]() 恒成立;
恒成立;
②函数的值域为![]() ;
;
③若![]() ,则一定
,则一定![]() ;
;
④对任意的![]() ,若函数
,若函数![]() 恒成立,则当
恒成立,则当![]() 时,
时,![]() 或
或![]() .
.
其中正确的结论是____________(写出所有正确结论的序号).
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中,角
,其中,角![]() 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与![]() 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点![]() ,且
,且![]() .
.
(Ⅰ)若![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若点![]() 为线性约束条件
为线性约束条件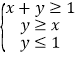 所围成的平面区域上的一个动点,试确定角
所围成的平面区域上的一个动点,试确定角![]() 的取值范围,并求函数
的取值范围,并求函数![]() 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=![]() AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.
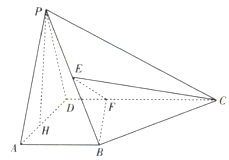
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=![]() ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com