
ЎҫМвДҝЎҝҫЭЖшПуЦРРД№ЫІмәНФӨІвЈә·ўЙъУЪ![]() өШөДЙііҫұ©Т»ЦұПтХэДП·ҪПтТЖ¶ҜЈ¬ЖдТЖ¶ҜЛЩ¶И
өШөДЙііҫұ©Т»ЦұПтХэДП·ҪПтТЖ¶ҜЈ¬ЖдТЖ¶ҜЛЩ¶И![]() УлКұјд
УлКұјд![]() өДәҜКэНјПсИзНјЛщКҫЈ¬№эПЯ¶О
өДәҜКэНјПсИзНјЛщКҫЈ¬№эПЯ¶О![]() ЙПТ»өг
ЙПТ»өг![]() ЧчәбЦбөДҙ№ПЯ
ЧчәбЦбөДҙ№ПЯ![]() Ј¬МЭРО
Ј¬МЭРО![]() ФЪЦұПЯ
ФЪЦұПЯ![]() ЧуІаІҝ·ЦөДГж»эјҙОӘ
ЧуІаІҝ·ЦөДГж»эјҙОӘ![]() ДЪЙііҫұ©Лщҫӯ№эөДВ·іМ
ДЪЙііҫұ©Лщҫӯ№эөДВ·іМ![]() .
.

ЈЁ1Ј©өұ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©Ҫ«![]() Лж
Лж![]() ұд»ҜөД№жВЙУГКэС§№ШПөКҪұнКҫіцАҙЈ»
ұд»ҜөД№жВЙУГКэС§№ШПөКҪұнКҫіцАҙЈ»
ЈЁ3Ј©Иф![]() іЗО»УЪ
іЗО»УЪ![]() өШХэДП·ҪПтЈ¬ЗТҫа
өШХэДП·ҪПтЈ¬ЗТҫа![]() өШ650
өШ650![]() Ј¬КФЕР¶ПХвіЎЙііҫұ©КЗ·с»бЗЦП®өҪ
Ј¬КФЕР¶ПХвіЎЙііҫұ©КЗ·с»бЗЦП®өҪ![]() іЗЈ¬Из№ы»бЈ¬ФЪЙііҫұ©·ўЙъәу¶аіӨКұјдЛьҪ«ЗЦП®өҪ
іЗЈ¬Из№ы»бЈ¬ФЪЙііҫұ©·ўЙъәу¶аіӨКұјдЛьҪ«ЗЦП®өҪ![]() іЗЈҝИз№ыІ»»бЈ¬ЗлЛөГчАнУЙ.
іЗЈҝИз№ыІ»»бЈ¬ЗлЛөГчАнУЙ.
Ўҫҙр°ёЎҝЈЁ1Ј©24Ј»ЈЁ2Ј©sЈҪ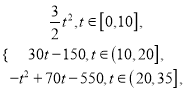 Ј»ЈЁ3Ј©Йііҫұ©·ўЙъ30 hәуҪ«ЗЦП®өҪNіЗ.
Ј»ЈЁ3Ј©Йііҫұ©·ўЙъ30 hәуҪ«ЗЦП®өҪNіЗ.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ПИЗуіцПЯ¶ОOAөДҪвОцКҪОӘv=4tЈ¬И»әу°Сt=10ЦұҪУҙъИлЗуіцҙЛКұөДЛЩ¶ИЈ¬јҙҝЙЗуіцSЈЁtЈ©өДЦөЈ»ЈЁ2Ј©ПИ·Ц¶ОЗуіцЛЩ¶ИvУлКұјдtөДәҜКэәҜКэ№ШПөЈ¬ФЩ·ЦұріЛТФКұјдјҙҝЙЗуөГ¶ФУҰөДәҜКэSЈЁtЈ©өДҪвОцКҪЈ»ЈЁ3Ј©ПИУЙ·Ц¶ОәҜКэөДҪвОцКҪТФј°¶ФУҰөД¶ЁТеУтҝЙТФЗуөГЖдЧоҙуЦөЈ¬·ўПЦЖдЧоҙуЦөҙуУЪ650Ј¬јҙҝЙПВҪбВЫ»бЗЦП®өҪNіЗЈ¬ФЩ°СSЈЁtЈ©=650ҙъИлјҙҝЙЗуіц¶ФУҰөДtЈ®
КФМвҪвОцЈәҪвЈәЈЁ1Ј©УЙНјПсҝЙЦӘЈ¬өұtЈҪ4КұЈ¬vЈҪ3ЎБ4ЈҪ12Ј¬
ЛщТФSЈҪ![]() ЎБ4ЎБ12ЈҪ24 kmЈ®
ЎБ4ЎБ12ЈҪ24 kmЈ®
ЈЁ2Ј©өұ0ЎЬtЎЬ10КұЈ¬SЈҪ![]() ЎӨtЎӨ3tЈҪ
ЎӨtЎӨ3tЈҪ![]() Ј»
Ј»
өұ10<tЎЬ20КұЈ¬SЈҪ![]() ЎБ10ЎБ30Ј«30ЈЁtЈӯ10Ј©ЈҪ30tЈӯ150Ј»
ЎБ10ЎБ30Ј«30ЈЁtЈӯ10Ј©ЈҪ30tЈӯ150Ј»
өұ20<tЎЬ35КұЈ¬SЈҪ![]() ЎБ10ЎБ30Ј«10ЎБ30Ј«ЈЁtЈӯ20Ј©ЎБ30Јӯ
ЎБ10ЎБ30Ј«10ЎБ30Ј«ЈЁtЈӯ20Ј©ЎБ30Јӯ![]() ЎБЈЁtЈӯ20Ј©ЎБ2ЈЁtЈӯ20Ј©ЈҪ
ЎБЈЁtЈӯ20Ј©ЎБ2ЈЁtЈӯ20Ј©ЈҪ![]() Ј®
Ј®
ЧЫЙПҝЙЦӘЈ¬ 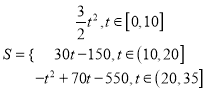 Ј®
Ј®
ЈЁ3Ј©ТтОӘөұtЎК[0Ј¬10]КұЈ¬SmaxЈҪ![]() ЎБ102ЈҪ150<650Ј¬
ЎБ102ЈҪ150<650Ј¬
өұtЎКЈЁ10Ј¬20]КұЈ¬SmaxЈҪ30ЎБ20Јӯ150ЈҪ450<650Ј¬
ЛщТФөұtЎКЈЁ20Ј¬35]КұЈ¬Бо![]() Ј¬ҪвөГ
Ј¬ҪвөГ![]() Ј®ТтОӘ20<tЎЬ35Ј¬ЛщТФtЈҪ30Ј®
Ј®ТтОӘ20<tЎЬ35Ј¬ЛщТФtЈҪ30Ј®
№КЙііҫұ©·ўЙъ30 hәуҪ«ЗЦП®өҪNіЗЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІCЈә ![]() =1ЈЁaЈҫ0Ј©өДҪ№өгФЪxЦбЙПЈ¬ЗТНЦФІCөДҪ№ҫаОӘ2Ј® ЈЁўсЈ©ЗуНЦФІCөДұкЧј·ҪіМЈ»
=1ЈЁaЈҫ0Ј©өДҪ№өгФЪxЦбЙПЈ¬ЗТНЦФІCөДҪ№ҫаОӘ2Ј® ЈЁўсЈ©ЗуНЦФІCөДұкЧј·ҪіМЈ»
ЈЁўтЈ©№эөгRЈЁ4Ј¬0Ј©өДЦұПЯlУлНЦФІCҪ»УЪБҪөгPЈ¬QЈ¬№эPЧчPNЎНxЦбЗТУлНЦФІCҪ»УЪБнТ»өгNЈ¬FОӘНЦФІCөДУТҪ№өгЈ¬ЗуЦӨЈәИэөгNЈ¬FЈ¬QФЪН¬Т»МхЦұПЯЙПЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©=x3©Ғ3x2 Ј® ЈЁўсЈ© ЗуfЈЁxЈ©өДөҘөчЗшјдЈ»
ЈЁўтЈ© ИфfЈЁxЈ©өД¶ЁТеУтОӘ[©Ғ1Ј¬m]КұЈ¬ЦөУтОӘ[©Ғ4Ј¬0]Ј¬ЗуmөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,ФЪИэАвЧ¶P-ABCЦР,PAЎНAB,PAЎНBC,AB=BC,DОӘПЯ¶ОACөДЦРөг.

(1)ЗуЦӨ:PAЎНBD.
(2)ЗуЦӨ:BDЎНЖҪГжPAC.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬ПтБҝ
Ј¬ПтБҝ![]() Ј¬
Ј¬ ![]() .
.
ЈЁ1Ј©ЗуәҜКэ![]() өДҪвОцКҪЈ¬ІўЗуөұ
өДҪвОцКҪЈ¬ІўЗуөұ![]() КұЈ¬
КұЈ¬ ![]() өДөҘөчөЭФцЗшјдЈ»
өДөҘөчөЭФцЗшјдЈ»
ЈЁ2Ј©өұ![]() КұЈ¬
КұЈ¬ ![]() өДЧоҙуЦөОӘ5Ј¬Зу
өДЧоҙуЦөОӘ5Ј¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ3Ј©өұ![]() КұЈ¬ИфІ»өИКҪ
КұЈ¬ИфІ»өИКҪ![]() ФЪ
ФЪ![]() ЙПәгіЙБўЈ¬ЗуКөКэ
ЙПәгіЙБўЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИэИЛ¶АБўЖЖТлН¬Т»·ЭГЬВлЈ®ТСЦӘИэИЛёчЧФЖЖТліцГЬВлөДёЕВК·ЦұрОӘ ![]() Ј¬ЗТЛыГЗКЗ·сЖЖТліцГЬВл»ҘІ»У°ПмЈ® ЈЁўсЈ©ЗуЗЎУР¶юИЛЖЖТліцГЬВлөДёЕВКЈ»
Ј¬ЗТЛыГЗКЗ·сЖЖТліцГЬВл»ҘІ»У°ПмЈ® ЈЁўсЈ©ЗуЗЎУР¶юИЛЖЖТліцГЬВлөДёЕВКЈ»
ЈЁўтЈ©Ў°ГЬВлұ»ЖЖТлЎұУлЎ°ГЬВлОҙұ»ЖЖТлЎұөДёЕВКДДёцҙуЈҝЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»Н¬С§ФЪөзДФЦРҙтіцИзПВИфёЙёцИҰЈәЎрЎсЎрЎрЎсЎрЎрЎрЎсЎрЎрЎрЎрЎсЎрЎрЎрЎрЎрЎсЎӯИфҪ«ҙЛИфёЙёцИҰТАҙЛ№жВЙјМРшПВИҘЈ¬өГөҪТ»ПөБРөДИҰЈ¬ДЗГҙФЪЗ°55ёцИҰЦРөДЎсөДёцКэКЗЈЁ Ј©
A.10
B.9
C.8
D.11
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©=x3©Ғ3x2©Ғ9x+2Ј®
ЈЁ1Ј©ЗуәҜКэfЈЁxЈ©өДөҘөчЗшјдЈ»
ЈЁ2Ј©ЗуәҜКэfЈЁxЈ©ФЪЗшјд[©Ғ1Ј¬m]ЈЁmЈҫ©Ғ1Ј©өДЧоРЎЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪ12јюН¬АаРНөДБгјюЦРУР2јюҙОЖ·Ј¬ійИЎ3ҙОҪшРРјмСйЈ¬ГҝҙОійИЎ1јюЈ¬ІўЗТИЎіцәуІ»ФЩ·Е»ШЈ¬ИфТФҰОәНҰЗ·ЦұрұнКҫИЎөҪөДҙОЖ·КэәНХэЖ·КэЈ®
ЈЁ1Ј©ЗуҰОөД·ЦІјБРЎўҫщЦөәН·ҪІоЈ»
ЈЁ2Ј©ЗуҰЗөД·ЦІјБРЎўҫщЦөәН·ҪІоЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com