练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，M、N、P为正方体AC1的棱AA1、A1B1、A1D1的中点，现沿截面MNP切去锥体A1-MNP，则剩余几何体的侧视图（左视图）为（　　）
    分析：侧视图是光线从几何体的侧面向左面正投影得到的投影图，结合三视图的作法，即可判断出其侧视图．
    解答：解：由侧视图的定义可知：点A1、P、M在后面的投影点分别是点B1、B1C1的中点、B1B的中点，
    线段PM在左面的投影面上的投影是以B1C1的中点、B1B的中点为端点的线段，且侧视图外框为正方形，
    即答案B正确．
    故选B．
    点评：本题考查三视图与几何体的关系，从正视图的定义可以判断出题中的侧视图，同时要注意能看见的轮廓线和棱用实线表示，不能看见的轮廓线和棱用虚线表示．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

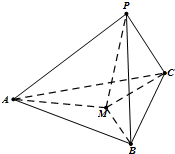    精英家教网如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
    1
    2
    ，x，y），且
    1
    x
    +
    a
    y
    ≥8恒成立，则正实数a的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

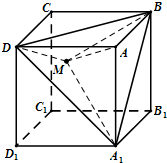    精英家教网如图，在单位正方体ABCD-A1B1C1D1中，设M是△A1BD内任一点（不包括边界），定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积．若f(M)=(
    112
    ，x，y)    ，且ax+y-108xy≥0恒成立，则正实数a的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=5，PB=4，PC=3．设点M为底面ABC内一点，定义f（M）=（m，n，p），其中m，n，p分别为三棱锥M-PAB、M-PBC、M-PCA的体积．若f（M）=（4，3x，3y），且ax-8xy+y≥0恒成立，则正实数a的取值范围是
    [9，+∞）
    [9，+∞）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=6，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m，n，p分别是三棱锥M-PAB，三棱锥M-PBC，三棱锥M-PCA的体积．若f（M）=（
    5
    3
    ，x，y），且
    1
    x
    +
    a
    y
    ≥27恒成立，则正实数a的最小值为
    4
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

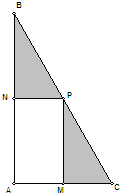    （2012•浦东新区一模）世博中学为了落实上海市教委推出的“阳光运动一小时”活动，计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地，如图点M在AC上，点N在AB上，且P点在斜边BC上，已知∠ACB=60°且|AC|=30米，|AM|=x，x∈[10，20]．
    （1）试用x表示S，并求S的取值范围；
    （2）设矩形AMPN健身场地每平方米的造价为
    37k
    		S
    ，再把矩形AMPN以外（阴影部分）铺上草坪，每平方米的造价为
    12k
    		S
    （k为正常数），求总造价T关于S的函数T=f（S）；试问如何选取|AM|的长使总造价T最低（不要求求出最低造价）．

    查看答案和解析>>

    同步练习册答案