
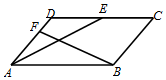
 如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.
如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$. 分析 根据向量的加减的几何意义和向量的数量积公式即可求出cos∠BAD,再根据同角的三角函数的关系即可求出sin∠BAD.
解答 解:在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{BF}$=$\overrightarrow{AF}$-$\overrightarrow{AB}$=$\frac{2}{3}$$\overrightarrow{AD}$-$\overrightarrow{AB}$,
∴$\overrightarrow{AE}$•$\overrightarrow{BF}$=($\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$)•($\frac{2}{3}$$\overrightarrow{AD}$-$\overrightarrow{AB}$)
=$\frac{2}{3}$${\overrightarrow{AD}}^{2}$-$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{2}{3}$$\overrightarrow{AD}$•$\overrightarrow{AB}$=$\frac{2}{3}$${\overrightarrow{AD}}^{2}$-$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{2}{3}$|$\overrightarrow{AD}$|•|$\overrightarrow{AB}$|cos∠BAD=6-8-8cos∠BAD=-4,
∴cos∠BAD=$\frac{1}{4}$,
∴sin∠BAD=$\frac{\sqrt{15}}{4}$,
故答案为:$\frac{\sqrt{15}}{4}$
点评 本题考查了向量的加减的几何意义和向量的数量积公式,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,则m⊥n | B. | 若α∥β,则m∥n | C. | 若m⊥n,则α⊥β | D. | 若n⊥α,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年 级 性 别 | 高一年级 | 高二年级 | 高三年级 |
| 男 | 520 | y | 400 |
| 女 | x | 610 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an}是等差数列且$\left\{{\frac{a_n}{n}}\right\}$递增 | |
| B. | Sn是等差数列{an}的前n项和,且$\left\{{\frac{S_n}{n}}\right\}$递增 | |
| C. | {an}是等比数列,公比为q>1 | |
| D. | 等比数列{an},公比为0<q<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
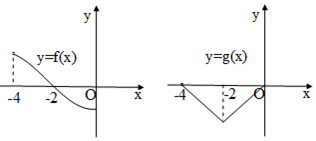 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
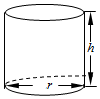 某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.
某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com