
| A. | a2<b2 | B. | $\sqrt{-a}<\sqrt{b}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | $\frac{a}{b}$+$\frac{b}{a}$≥2 |
分析 根据题意,依次分析选项,对于A、B,举出反例可得其错误,对于C,分析可得$\frac{1}{a}$<0而$\frac{1}{b}$>0,易得C正确,对于D,分析a、b的符号可得$\frac{a}{b}$<0且$\frac{b}{a}$<0,则有$\frac{a}{b}$+$\frac{b}{a}$<0,可得D错误;综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、若a=-3,而b=1,则a2>b2.故A错误;
对于B、若a=-9,而b=1,则有$\sqrt{-(-9)}$>$\sqrt{a}$,故B错误;
对于C,若a<0,则$\frac{1}{a}$<0,而b>0,则$\frac{1}{b}$>0,故$\frac{1}{a}$<$\frac{1}{b}$,故C正确;
对于D,若a<0,b>0,故$\frac{a}{b}$<0,$\frac{b}{a}$<0,则有$\frac{a}{b}$+$\frac{b}{a}$<0,故D错误;
故选C.
点评 本题考查不等式的性质,关键是熟悉不等式的性质,对于不成立的不等式,可以举出反例,进行判断.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
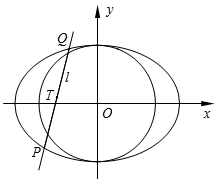 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com