
����Ŀ��ij���������ϵͳ��60%����Ȼ��ѧ����Ŀ��40%���Ļ���������Ŀ(��������е���Ŀ�����dz���)���������������г�ȡ3����Ŀ���������ֳ�ȡ����������һ��ֱ�Ӵ�����������ȡ3����Ŀ������������������а�����Ŀ�����÷ֲ�����ķ�����ȡ10����Ŀ��Ϊ�������ٴ���10����Ŀ�������ȡ3����Ŀ��
(1)���ַ�����ȡ��3����Ŀ�У�ǡ����1����Ȼ��ѧ����Ŀ��2���Ļ���������Ŀ�ĸ����Ƿ���ͬ?����ͬ��˵�����ɣ�����ͬ���ֱ��������ֳ�ȡ������Ӧ�ĸ��ʣ�
(2)��֪ij�����߳�ȡ��3����Ŀǡ����1����Ȼ��ѧ����Ŀ��2���Ļ���������Ŀ���Ҹò����ߴ����Ȼ��ѧ����Ŀ�ĸ���Ϊ![]() ������Ļ���������Ŀ�ĸ���Ϊ
������Ļ���������Ŀ�ĸ���Ϊ![]() ����ò����ߴ�Ե���Ŀ��ΪX����X�ķֲ��к���ѧ������
����ò����ߴ�Ե���Ŀ��ΪX����X�ķֲ��к���ѧ������
���𰸡���1�����ֳ�ȡ�����õ��ĸ��ʲ�ͬ��2��������
��������
��1���ֱ�������ַ����¸��ʣ��ٱȽϣ���2����ȷ������������ٷֱ����Ӧ���ʣ��б��÷ֲ��У���������ѧ������ʽ������.
(1)���ֳ�ȡ�����õ��ĸ��ʲ�ͬ��
����һ�������������Ŀ�����dz�������Ϊÿ��ȡ1����Ŀ���鵽��Ȼ��ѧ����Ŀ�ĸ��ʾ�Ϊ![]() ���鵽�Ļ���������Ŀ�ĸ��ʾ�Ϊ
���鵽�Ļ���������Ŀ�ĸ��ʾ�Ϊ![]() �����Գ�ȡ��3����Ŀ��ǡ����1����Ȼ��ѧ����Ŀ��2���Ļ���������Ŀ�ĸ���Ϊ
�����Գ�ȡ��3����Ŀ��ǡ����1����Ȼ��ѧ����Ŀ��2���Ļ���������Ŀ�ĸ���Ϊ![]() ��
��![]() (
(![]() )
)![]() =
=![]() ��
��
��������������Ŀ�����÷ֲ������ȡ��10����Ŀ����6����Ȼ��ѧ����Ŀ��4���Ļ���������Ŀ������10����Ŀ�г�ȡ3����Ŀ��ǡ����1����Ȼ��ѧ����Ŀ��2���Ļ���������Ŀ�ĸ���Ϊ![]() =
=![]()
(2)������ã�X�����п���ȡֵΪ0��1��2��3��
P(X=0)=![]() =
=![]() ��
��
P(X=1)=![]() +
+![]() +
+![]() =
=![]()
P(X=2)=![]() +
+![]() +
+![]() =
=![]() ��P(X=3)=
��P(X=3)= ![]() =
=![]() ��
��
����X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X����ѧ����E(X)=0��![]() +1��
+1��![]() +2��
+2��![]() +3��
+3��![]() =
=![]() ��
��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������������������ĸ��ʵ���ͬ��С���ĸ�С���ĺ���ֱ�Ϊ1��1��2��3���ּס�����λͬѧ���δ������������ȡһ������������º��벢�Żأ�
��������ס�����λͬѧ�������������ͬ�ĸ��ʣ�
������������������������������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵԭ��OΪ���㣬��x��Ǹ�����Ϊ���ᣬ��ƽ��ֱ������ϵ�ij��ȵ�λΪ���ȵ�λ����������ϵ����ֱ֪��l�IJ�������Ϊ ![]() ��tΪ������������C�ļ����귽��Ϊ��sin2��=4cos��
��tΪ������������C�ļ����귽��Ϊ��sin2��=4cos��
���� ������C��ֱ�����귽�̣�
���� ��ֱ��l������C�ཻ��A��B���㣬��|AB|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ͼ��ͼ��ʾ�������������ĸ����������������ĺ����ǣ� �� 
A.f��x��=x2
B.f��x��=sinx
C.f��x��=ex
D.f��x��= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��0��b��0�� ��
A.��lna+2a=lnb+3b����a��b
B.2a+2a=2b+3b����a��b
C.��lna��2a=lnb��3b����a��b
D.2a��2a=2b��3b����a��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin��xcos��x��cos2��x��
sin��xcos��x��cos2��x�� ![]() ���أ�0��x��R����ͼ��������������ߵ�ľ���Ϊ�У�
���أ�0��x��R����ͼ��������������ߵ�ľ���Ϊ�У�
��������f��x���ĵ����������䣻
��������ABC�����ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����c= ![]() ��f��C��=0��sinB=3sinA����a��b��ֵ��
��f��C��=0��sinB=3sinA����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������ɸ���ڳ�������ͼ����ÿ���ߣ����������˵㣩n��n��1��n��N*�����㣬��Ӧ��ͼ�����ܵĵ�����Ϊan �� �� ![]() +
+ ![]() +
+ ![]() +��+
+��+ ![]() = ��
= �� 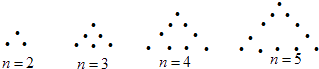
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��f(x)�Ķ�����Ϊ(0������)���Ҷ�һ��x>0��y>0����f![]() ��f(x)��f(y)����x>1ʱ����f(x)>0��
��f(x)��f(y)����x>1ʱ����f(x)>0��
(1)��f(1)��ֵ��
(2)�ж�f(x)�ĵ����Բ�֤����
(3)��f(6)��1���ⲻ��ʽf(x��3)��f![]() <2��
<2��
(4)��f(4)��2����f(x)��[1,16]�ϵ�ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com